Phương pháp giải:

Đặt x=1-t

Sử dụng phương pháp đổi biến.

Biến đổi biểu thức dưới dấu tích phân tìm $f\left( x \right)$

Lời giải chi tiết:

$I = \int\limits_0^1 {\frac{{dx}}{{1 + f\left( x \right)}}}$

Đặt x=1-t

$\Rightarrow dx =  - dt$

Đổi cận

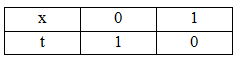
$\begin{array}{l} =  > I = \int\limits_1^0 {\frac{{ - dt}}{{1 + f\left( {1 - t} \right)}}}  = \int\limits_0^1 {\frac{{dt}}{{1 + \frac{1}{{f\left( t \right)}}}}} \\ = \int\limits_0^1 {\frac{{f\left( x \right)}}{{1 + f\left( x \right)}}dx} \end{array}$

Mà $I = \int\limits_0^1 {\frac{{dx}}{{1 + f\left( x \right)}}}$

Vậy $\frac{{f\left( x \right)}}{{1 + f\left( x \right)}} = \frac{1}{{1 + f\left( x \right)}} \Leftrightarrow f\left( x \right) = 1$

$\Rightarrow I = 1$.