Câu hỏi:
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\,\,\left( {a \ne 0} \right)\), đồ thị hàm số \(f'\left( x \right)\) như hình vẽ bên dưới.
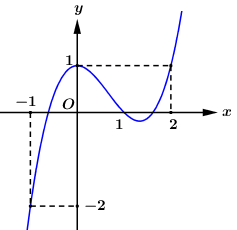
Đặt \(g\left( x \right) = f\left( x \right) - \dfrac{{2{x^3}}}{6} + {x^2} - x + 2020\), khẳng định nào sau là đúng?
- A Hàm số \(g\left( x \right)\) có hai điểm cực tiểu và một điểm cực đại.
- B Hàm số \(g\left( x \right)\) có hai điểm cực đại và một điểm cực tiểu.
- C Hàm số \(g\left( x \right)\) có đúng hai cực trị.
- D Hàm số \(g\left( x \right)\) có đúng một cực trị.
Phương pháp giải:
- Tìm đạo hàm của \(y = g\left( x \right)\).
- Giải phương trình \(g'\left( x \right) = 0\) dựa vào tương giao đồ thị hàm số.
- Lập bảng biến thiên hàm số \(y = g\left( x \right)\) rồi kết luận các điểm cực trị của hàm số.
Lời giải chi tiết:
Ta có \(g\left( x \right) = f\left( x \right) - \dfrac{{2{x^3}}}{6} + {x^2} - x + 2020\) \( \Rightarrow g'\left( x \right) = f'\left( x \right) - {x^2} + 2x - 1\).
Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 2x + 1\).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và \(y = {x^2} - 2x + 1\).
Vẽ hai đồ thị hàm số \(y = f'\left( x \right)\) và \(y = {x^2} - 2x + 1\) trên cùng mặt phẳng tọa độ ta có:
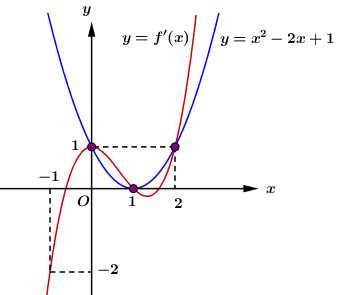
Dựa vào đồ thị hàm số ta thấy \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 2\end{array} \right.\).
Ta có BBT hàm số \(y = g\left( x \right)\) như sau:
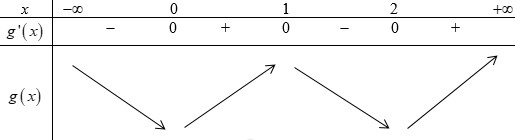
Dựa vào bảng biến thiên ta thấy hàm số \(y = g\left( x \right)\) có 2 điêm cực tiểu và 1 điểm cực đai.
Chọn A.


















