Phương pháp giải:

Sử dụng khái niệm về mặt phẳng đối xứng của khối đa diện đều.

Lời giải chi tiết:

Ta có:  Ba mặt \(ABC,\,\,ACD,\,\,ADB\) là ba tam giác bằng nhau và cân tại định \(A\)

\( \Rightarrow \left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\)

TH1: Ta có: \(\left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\)  và các cạnh bên không bằng các cạnh đáy

Khi đó ta có các mặt phẳng đối xứng là: \(\left( {ABN} \right),\,\,\left( {ACM} \right),\,\,\left( {ADP} \right)\) với \(M,\,\,N,\,\,P\) lần lượt là trung điểm của các cạnh \(BD,\,\,DC,\,\,BC.\)

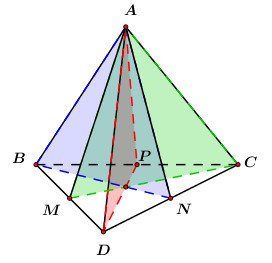
 TH2: Ta có: \(\left\{ \begin{array}{l}AB = AC = AD\\BC = CD = BD\end{array} \right.\)  và các cạnh bên bằng các cạnh đáy

Khi đó ta có các mặt đối xứng như TH1 và thêm các mặt phẳng \(\left( {EDC} \right),\,\,\left( {FBD} \right),\,\,\left( {HBC} \right)\) với \[E,\,\,F,\,\,H\] lần lượt là trung điểm của các cạnh \(AB,\,\,AC,\,\,AD.\)

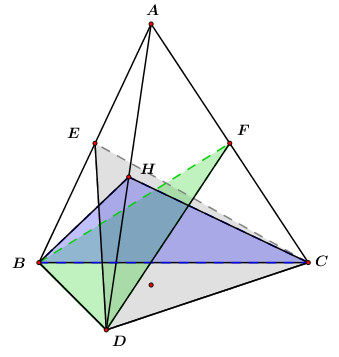
Chọn C.