Câu hỏi:
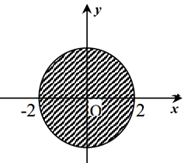
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\) Để điểm biểu diễn hình học của \(z\) nằm trong hình tròn như hình vẽ (không tính biên), điều kiện của \(a\) và \(b\) là:
- A \({a^2} + {b^2} < 4\)
- B \({a^2} + {b^2} \le 4\)
- C \({a^2} + {b^2} > 4\)
- D \({a^2} + {b^2} \ge 4\)
Phương pháp giải:
Điểm biểu diễn số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) là \(M\left( {a;\,\,b} \right).\)
Dựa vào đồ thị hàm số, viết phương trình đường tròn trên đồ thị.
Lời giải chi tiết:
Điểm biểu diễn số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) là \(M\left( {a;\,\,b} \right).\)
Ta thấy tập hợp các điểm biểu diễn số phức \(z\) bài cho là hình tròn (không chứa biên) có tâm \(O\) và bán kính \(R = 2\)
\( \Rightarrow \) Điều kiện thỏa mãn bài toán là: \({a^2} + {b^2} < 4.\)
Chọn A.
Quảng cáo
Câu hỏi trước
