Câu hỏi:
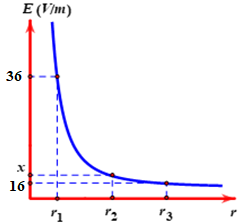
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết: \(2{{r}_{2}}={{r}_{1}}+{{r}_{3}}\) . Tìm x?
- A 25V/m
- B 30V/m
- C 23,04V/m
- D 28,02V/m
Phương pháp giải:
Áp dụng công thức tính cường độ điện trường: \(E=k.\frac{\left| q \right|}{\varepsilon {{r}^{2}}}\)
Vì điểm M là trung điểm của A và B nên: \({{r}_{M}}=\frac{{{r}_{A}}+{{r}_{B}}}{2}\)
Cường độ điện trường tại M: \(\frac{1}{\sqrt{{{E}_{M}}}}=\frac{1}{2}\left( \frac{1}{\sqrt{{{E}_{A}}}}+\frac{1}{\sqrt{{{E}_{B}}}} \right)\)
Lời giải chi tiết:
Ta có: \(2{{r}_{2}}={{r}_{1}}+{{r}_{3}}\Rightarrow {{r}_{2}}=\frac{{{r}_{1}}+{{r}_{3}}}{2}\) \(\Rightarrow {{r}_{2}}\) là trung điểm của \({{r}_{1}}{{r}_{3}}\)
Áp dụng công thức tính cường độ điện trường tại trung điểm ta có:
\(\frac{1}{\sqrt{{{E}_{2}}}}=\frac{1}{2}\left( \frac{1}{\sqrt{{{E}_{1}}}}+\frac{1}{\sqrt{{{E}_{3}}}} \right)\)
Thay số ta được:
\(\frac{1}{\sqrt{x}}=\frac{1}{2}\left( \frac{1}{\sqrt{16}}+\frac{1}{\sqrt{36}} \right)\Rightarrow x=23,04V/m\)
Chọn C.


















