 Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
50 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng cao
Câu hỏi:
Dao động của một chất điểm có khối lượng \(100\,\,g\) là tổng hợp của hai dao động cùng phương, có phương trình lần lượt là \({x_1} = {A_1}\cos \left( {10\pi t + {\varphi _1}} \right)\) và \({x_2} = {A_2}\cos \left( {10\pi t + {\varphi _2}} \right)\) (\(t\) tính bằng \(s\)). Hình bên là đồ thị biểu diễn mối liên hệ của \({x_1}\) và \({x_2}\). Động năng cực đại của chất điểm là
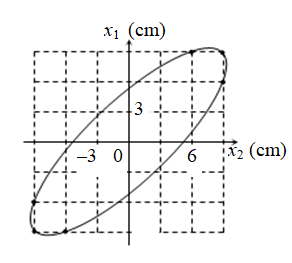
- A \(0,405\,\,J\).
- B \(1,60\,\,J\).
- C \(0,442\,\,J\).
- D \(0,81\,\,J\).
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thị và giản đồ vecto
Biên độ dao động cực đại: \(A=\sqrt{{{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }\)
Động năng cực đại của chất điểm: \({{\text{W}}_{d\max }}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)
Lời giải chi tiết:
Từ đồ thị ta lấy 2 điểm với \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=9cm \\\end{align} \right.\) và \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=6cm \\\end{align} \right.\), ta có giản đồ vecto:

Trường hợp \({{x}_{1}}={{x}_{2}}=9cm\), ta có: \(x=A\cos \frac{\Delta \varphi }{2}\Rightarrow \Delta \varphi =2\text{ar}\cos \frac{9}{A}\)
Với \(\left\{ \begin{align}& {{x}_{1}}=9cm \\& {{x}_{2}}=6cm \\\end{align} \right.\), ta có: \(\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\text{ar}\cos \frac{6}{A}-\text{ar}\cos \frac{9}{A}\)
\(\Rightarrow \Delta \varphi =2\text{ar}\cos \frac{9}{A}=\text{ar}\cos \frac{6}{A}-\text{ar}\cos \frac{9}{A}\)
Sử dụng chức năng SHIFT+SOLVE trong máy tính bỏ túi, ta có:
\(A\approx 9,4\,\,\left( cm \right)\Rightarrow \Delta \varphi =33,{{55}^{0}}\)
Biên độ dao động tổng hợp là:
\({{A}_{0}}=\sqrt{2{{A}^{2}}+2{{A}^{2}}\cos \Delta \varphi }\approx 18\,\,\left( cm \right)\)
Động năng cực đại của vật là:
\({{\text{W}}_{d\max }}=\frac{1}{2}m{{\omega }^{2}}{{A}_{0}}^{2}=\frac{1}{2}.0,1.{{\left( 10\pi \right)}^{2}}.0,{{18}^{2}}=1,62\,\,\left( J \right)\)
Chọn B.

















