Phương pháp giải:

Lời giải chi tiết:

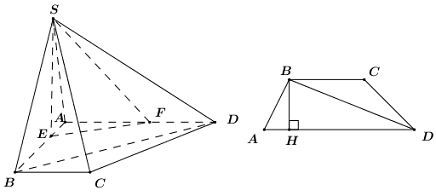
Đặt \(\dfrac{{AE}}{{AB}} = x,\,\,\dfrac{{AF}}{{AD}} = y\,\,\left( {0 < x,\,\,y \le 1} \right)\). Theo bài ra ta có: \(\dfrac{{3AB}}{{AE}} + \dfrac{{AD}}{{AF}} = 5\) \( \Rightarrow \dfrac{3}{x} + \dfrac{1}{y} = 5\,\,\,\left( 1 \right)\).

Vì hai khối chóp \(S.BCDFE\) và \(S.ABCD\) có cùng chiều cao nên \(k = \dfrac{{{V_{S.BCDFE}}}}{{{V_{S.ABCD}}}} = \dfrac{{{S_{BCDFE}}}}{{{S_{ABCD}}}}\).

Đặt \({S_{ABCD}} = S\), kẻ \(BH \bot AD\,\,\left( {H \in AD} \right)\) ta có \(S = \dfrac{1}{2}BH.\left( {BC + AD} \right) = \dfrac{3}{2}.BH.BC\).

Ta có: \(\dfrac{{{S_{AEF}}}}{{{S_{ABD}}}} = \dfrac{{\dfrac{1}{2}AE.AF.\sin \angle BAD}}{{\dfrac{1}{2}AB.AD.\sin \angle BAD}} = xy \Rightarrow {S_{AEF}} = xy.{S_{ABD}}\).

Mà \({S_{ABD}} = \dfrac{1}{2}BH.AD\) nên \({S_{AEF}} = \dfrac{1}{2}xy.BH.AD = xy.BH.BC = \dfrac{3}{2}BH.BC.\dfrac{2}{3}xy\) \( \Rightarrow {S_{AEF}} = \dfrac{2}{3}xy.S\).

\( \Rightarrow {S_{BCDFE}} = {S_{ABCD}} - {S_{AEF}} = S - \dfrac{2}{3}xy.S = S\left( {1 - \dfrac{2}{3}xy} \right)\).

\( \Rightarrow k = \dfrac{{S.\left( {1 - \dfrac{2}{3}xy} \right)}}{S} = 1 - \dfrac{2}{3}xy\).

Theo (1) ta có: \(\dfrac{3}{x} + \dfrac{1}{y} = 5 \Leftrightarrow y = \dfrac{x}{{5x - 3}}\).

Ta có \(0 < \dfrac{x}{{5x - 3}} \le 1 \Leftrightarrow \left\{ \begin{array}{l}\dfrac{x}{{5x - 3}} > 0\\\dfrac{{x - 5x + 3}}{{5x - 3}} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 3 > 0\,\,\left( {do\,\,x > 0} \right)\\3 - 4x \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x > \dfrac{3}{5}\\x \ge \dfrac{3}{4}\end{array} \right. \Leftrightarrow x \ge \dfrac{3}{4}\).

Khi đó ta có

\(\begin{array}{l}k = 1 - \dfrac{2}{3}xy = 1 - \dfrac{2}{3}x.\dfrac{x}{{5x - 3}}\\\,\,\,\, = 1 - \dfrac{{2{x^2}}}{{3\left( {5x - 3} \right)}} = \dfrac{{15x - 9 - 2{x^2}}}{{3\left( {5x - 3} \right)}} = f\left( x \right)\end{array}\)

Xét hàm số \(f\left( x \right) = \dfrac{{ - 2{x^2} + 15x - 9}}{{3\left( {5x - 3} \right)}}\) với \(\dfrac{3}{4} \le x \le 1\) ta có:

\(\begin{array}{l}f'\left( x \right) = \dfrac{{\left( { - 4x + 15} \right).3\left( {5x - 3} \right) - \left( { - 2{x^2} + 15x - 9} \right).15}}{{9{{\left( {5x - 3} \right)}^2}}}\\f'\left( x \right) = \dfrac{{3\left( { - 20{x^2} + 87x - 45} \right) - \left( { - 30{x^2} + 225x - 135} \right)}}{{9{{\left( {5x - 3} \right)}^2}}}\\f'\left( x \right) = \dfrac{{ - 30{x^2} + 36x}}{{9{{\left( {5x - 3} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{6}{5}\,\,\left( {ktm} \right)\\x = 0\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)

BBT:

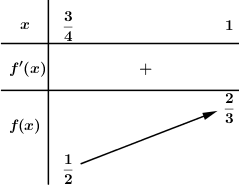
\( \Rightarrow {k_{\min }} = \dfrac{1}{2},\,\,{k_{\max }} = \dfrac{2}{3}\).

Vậy \({k_{\min }} + {k_{\max }} = \dfrac{1}{2} + \dfrac{2}{3} = \dfrac{7}{6}\).

Chọn D.