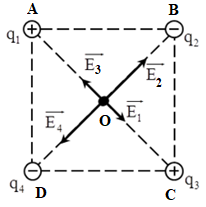
Câu hỏi:
Tại ba đỉnh A, B và C của một hình vuông ABCD cạnh \(6cm\) trong chân không, đặt ba điện tích điểm \(q_1 = q_3 = 2.10^{ - 7}C\,;\,\,q_2 = - 4.10^{ - 7}C.\) Xác định điện tích \({q_4}\) đặt tại D để cường độ điện trường tổng hợp gây bởi hệ điện tích tại tâm O bằng \(0.\)
- A \( {3.10^{ - 7}}C\)
- B \( - {3.10^{ - 7}}C\)
- C \({4.10^{ - 7}}C\)
- D \( - {4.10^{ - 7}}C\)
Phương pháp giải:
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
- Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\)
- Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\)
Lời giải chi tiết:
+ Cường độ điện trường tổng hợp tại O:\(\overrightarrow {{E_O}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} + \overrightarrow {{E_4}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} ;\overrightarrow {{E_4}} \) lần lượt là vecto cường độ điện trường do các điện tích \(q_1\,;\,q_2\,;\,q_3\,;\,q_4\) gây ra tại O.
+ Để cường độ điện trường tại O triệt tiêu thì \(\overrightarrow {{E_O}} = 0\)
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AO = CO \end{matrix}\right. \Rightarrow E_1 = E_3\)
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_3}} \\{E_1} = {E_3}\end{array} \right. \Rightarrow \overrightarrow {{E_{13}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_3}} = 0\)\( \Rightarrow \overrightarrow {{E_O}} = \overrightarrow {{E_2}} + \overrightarrow {{E_4}} \)
Để \(\overrightarrow {{E_O}} = 0 \Leftrightarrow \overrightarrow {{E_2}} + \overrightarrow {{E_4}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_2}} \uparrow \downarrow \overrightarrow {{E_4}} \,\,\left( 1 \right)\\{E_2} = {E_4}\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_4}} \) hướng lại gần \({q_4} \Rightarrow {q_4} < 0\)
Từ (2) ta có \({E_4} = {E_2} \Leftrightarrow \dfrac{{k\left| {{q_4}} \right|}}{{O{B^2}}} = \dfrac{{k\left| {{q_2}} \right|}}{{O{B^2}}}\)
\( \Rightarrow \left| {{q_4}} \right| = \left| {{q_2}} \right| = {4.10^{ - 7}}C \Rightarrow {q_4} = - {4.10^{ - 7}}C\)
Chọn D.