Phương pháp giải:

Lời giải chi tiết:

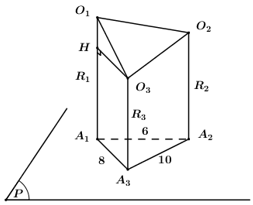
Do các mặt cầu tâm ${O_1},\,\,{O_2},\,\,{O_3}$ đôi một tiếp xúc ngoài nên ta có $\left\{ \begin{array}{l}{R_1} + {R_2} = {O_1}{O_2}\\{R_2} + {R_3} = {O_2}{O_3}\\{R_3} + {R_1} = {O_3}{O_1}\end{array} \right.$. 

Kẻ ${O_3}H \bot {O_1}A$, khi đó ${A_1}{A_3}{O_3}H$ là hình chữ nhật $\Rightarrow {A_1}H = {O_3}{A_3} = {R_3}$ $\Rightarrow {O_1}H = {O_1}{A_1} - {A_1}H = {R_1} - {R_3}$.

Áp dụng định lí Pytago ta có:

$\begin{array}{l}{O_1}{O_3}^2 = {O_1}{H^2} + {O_3}{H^2}\\ \Leftrightarrow {\left( {{R_1} + {R_3}} \right)^2} = {\left( {{R_1} - {R_3}} \right)^2} + {8^2}\\ \Leftrightarrow R_1^2 + 2{R_1}{R_3} + R_3^2 = R_1^2 - 2{R_1}{R_3} + R_3^2 + 64\\ \Leftrightarrow 4{R_1}{R_3} = 64 \Leftrightarrow {R_1}{R_3} = 16\end{array}$

Hoàn toàn tương tự ta chứng minh được ${R_1}{R_2} = 9,\,\,{R_2}{R_3} = 25$.

$\Rightarrow {\left( {{R_1}{R_2}{R_3}} \right)^2} = 3600 \Leftrightarrow {R_1}{R_2}{R_3} = 60$ $\Rightarrow {R_1} = \dfrac{{12}}{5},\,\,{R_2} = \dfrac{{15}}{4},\,\,{R_3} = \dfrac{{20}}{3}$.

Ta có hình vẽ chính xác như sau:

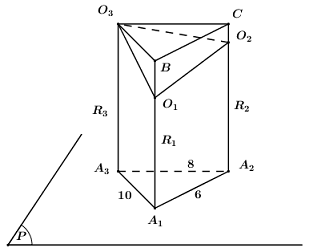
Dựng hình lăng trụ đứng ${A_1}{A_2}{A_3}.BC{O_3}$.

$\Rightarrow {V_{{A_1}{A_2}{A_3}.{O_1}{O_2}{O_3}}} = {V_{{A_1}{A_2}{A_3}.BC{O_3}}} - {V_{{O_3}.BC{O_2}{O_3}}}$.

Ta có: $B{O_1} = {R_3} - {R_1} = \dfrac{{64}}{{15}},\,\,C{O_2} = {R_3} - {R_2} = \dfrac{{35}}{{12}}$

${V_{{A_1}{A_2}{A_3}.BC{O_3}}} = {R_3}.\dfrac{1}{2}{A_2}{A_3}.{A_2}{A_1} = \dfrac{{20}}{3}.\dfrac{1}{2}.6.8 = 160$.

${S_{BC{O_2}{O_1}}} = \dfrac{1}{2}BC.\left( {C{O_2} + B{O_1}} \right) = \dfrac{1}{2}.6.\left( {\dfrac{{35}}{{12}} + \dfrac{{64}}{{15}}} \right) = \dfrac{{431}}{{20}}$.

Ta có $\left\{ \begin{array}{l}{O_3}C \bot BC\\{O_3}C \bot C{A_2}\end{array} \right. \Rightarrow {O_3}C \bot \left( {BC{O_2}{O_1}} \right)$.

$\Rightarrow {V_{{O_3}.BC{O_2}{O_1}}} = \dfrac{1}{3}{O_3}C.{S_{BC{O_2}{O_1}}} = \dfrac{1}{3}.8.\dfrac{{431}}{{20}} = \dfrac{{862}}{{15}}$.

Vậy $\Rightarrow {V_{{A_1}{A_2}{A_3}.{O_1}{O_2}{O_3}}} = {V_{{A_1}{A_2}{A_3}.BC{O_3}}} - {V_{{O_3}.BC{O_2}{O_3}}} = 160 - \dfrac{{862}}{{15}} = \dfrac{{1538}}{{15}}$.

Chọn D.