Câu hỏi:
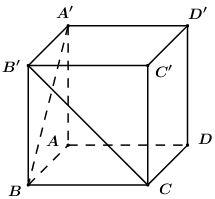
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có \(AB = 5a\), \(AD = 6a\), \(BD = 7a\), \(AA' = \dfrac{{12\sqrt 6 a}}{7}\). Khoảng cách giữa hai đường thẳng \(A'B\) và \(B'C\) là:
- A \(\dfrac{{12a}}{7}\)
- B \(\dfrac{{12\sqrt 2 a}}{7}\)
- C \(\dfrac{{12\sqrt 6 a}}{7}\)
- D \(\dfrac{{12\sqrt 3 a}}{7}\)
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song và chứa đường thẳng kia, chứng minh \(d\left( {A'B;B'C} \right) = d\left( {B'C;\left( {A'BD} \right)} \right) = d\left( {B;\left( {A'BD} \right)} \right)\).
- Đổi \(d\left( {B;\left( {A'BD} \right)} \right)\) sang \(d\left( {A;\left( {A'BD} \right)} \right)\).
- Trong \(\left( {ABCD} \right)\) kẻ \(AH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {A'AH} \right)\) kẻ \(AK \bot A'H\,\,\left( {K \in A'H} \right)\). Chứng minh \(AK \bot \left( {A'BD} \right)\).
- Sử dụng công thức He-rong \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(p\) là nửa chu vi, \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của tam giác, tính diện tích tam giác \(ABD\), từ đó tính chiều cao \(AH\).
- Sử dụng tính chất tam giác vuông cân hoặc hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Ta có \(B'C\parallel A'D \Rightarrow B'C\parallel \left( {A'BD} \right) \supset A'B\).
\( \Rightarrow d\left( {A'B;B'C} \right) = d\left( {B'C;\left( {A'BD} \right)} \right) = d\left( {B;\left( {A'BD} \right)} \right)\).
Gọi \(O = AB' \cap A'B\) suy ra \(O\) là trung điểm của \(AB'\).
Ta có: \(AB' \cap \left( {A'BD} \right) = O \Rightarrow \dfrac{{d\left( {B';\left( {A'BD} \right)} \right)}}{{d\left( {A;\left( {A'BD} \right)} \right)}} = \dfrac{{B'O}}{{AO}} = 1\) \( \Rightarrow d\left( {B';\left( {A'BD} \right)} \right) = d\left( {A;\left( {A'BD} \right)} \right)\).
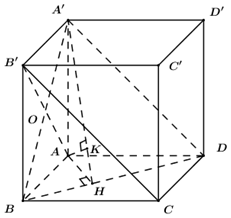
Trong \(\left( {ABCD} \right)\) kẻ \(AH \bot BD\,\,\left( {H \in BD} \right)\), trong \(\left( {A'AH} \right)\) kẻ \(AK \bot A'H\,\,\left( {K \in A'H} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AH\\BD \bot AA'\end{array} \right. \Rightarrow BD \bot \left( {A'AH} \right) \Rightarrow BD \bot AK\\\left\{ \begin{array}{l}AK \bot A'H\\AK \bot BD\end{array} \right. \Rightarrow AK \bot \left( {A'BD} \right) \Rightarrow d\left( {A;\left( {A'BD} \right)} \right) = AK\end{array}\)
Xét \(\Delta ABD\) có:
+ Nửa chu vi tam giác \(ABD\) là: \(p = \dfrac{{5a + 6a + 7a}}{2} = 9a\).
+ Diện tích tam giác \(ABD\) là: \({S_{ABD}} = \sqrt {p\left( {p - 5a} \right)\left( {p - 6a} \right)\left( {p - 7a} \right)} = 6\sqrt 6 {a^2}\).
+ Lại có: \({S_{ABD}} = \dfrac{1}{2}AH.BD \Rightarrow AH = \dfrac{{2{S_{ABD}}}}{{BD}} = \dfrac{{12\sqrt 6 a}}{7} = AA'\).
\( \Rightarrow \Delta A'AH\) vuông cân tại \(A\) \( \Rightarrow AK = \dfrac{{AH}}{{\sqrt 2 }} = \dfrac{{12\sqrt 3 a}}{7}\).
Vậy \(d\left( {A'B;B'C} \right) = \dfrac{{12\sqrt 3 a}}{7}\).
Chọn D.