Phương pháp giải:

Khối chóp có thể tích lớn nhất khi 3 cạnh đôi một vuông góc.

Lời giải chi tiết:

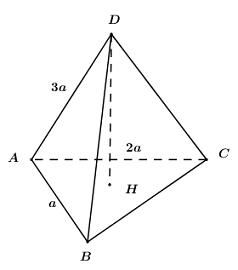
Giả sử khối chóp $ABCD$ có $AB = a,\,\,AC = 2a,\,\,AD = 3a$.

Gọi $H$ là hình chiếu vuông góc của $D$ lên $\left( {ABC} \right)$, khi đó ta có: $DH \bot \left( {ABC} \right)$ và $DH \le AD$.

Ta có: ${S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC \le \dfrac{1}{2}AB.AC$.

Vây ${V_{ABCD}} = \dfrac{1}{3}DH.{S_{\Delta ABC}} \le \dfrac{1}{3}AD.\dfrac{1}{2}AB.AC = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.a.2a.3a = {a^3}$.

Dấu “=” xảy ra $\Leftrightarrow AD \bot \left( {ABC} \right),\,\,AB \bot AC$ hay $AB,\,\,AC,\,\,AD$ đôi một vuông góc.

Chọn D.