Câu hỏi:
Tìm \(m\) để hàm số \(y = {x^3} - m{x^2} + x + 1\) nghịch biến trên \(\left( { - 2; - 1} \right)\)?
- A \(m \ge - \dfrac{{13}}{2}\)
- B \(m \le - \dfrac{{13}}{2}\)
- C \(m \le - \dfrac{{13}}{4}\)
- D \(m \ge - \dfrac{{13}}{4}\)
Phương pháp giải:
- Tính \(y'\).
- Để hàm số nghịch biến trên \(\left( { - 2; - 1} \right)\) thì \(y' \le 0\,\,\forall x \in \left( { - 2; - 1} \right)\).
- Cô lập \(m\), đưa bất phương trình về dạng \(m \le g\left( x \right)\,\,\forall x \in \left( { - 2; - 1} \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left[ { - 2; - 1} \right]} g\left( x \right)\).
- Lập BBT hàm số \(g\left( x \right)\) và kết luận.
Lời giải chi tiết:
Hàm số đã cho xác định trên \(\left( { - 2; - 1} \right)\).
Ta có: \(y' = 3{x^2} - 2mx + 1\).
Để hàm số nghịch biến trên \(\left( { - 2; - 1} \right)\) thì \(y' \le 0\,\,\forall x \in \left( { - 2; - 1} \right)\).
\(\begin{array}{l} \Leftrightarrow 3{x^2} - 2mx + 1 \le 0\,\,\forall x \in \left( { - 2; - 1} \right)\\ \Leftrightarrow 2mx \ge 3{x^2} + 1\,\,\forall x \in \left( { - 2; - 1} \right)\\ \Leftrightarrow 2m \le \dfrac{{3{x^2} + 1}}{x}\,\,\forall x \in \left( { - 2; - 1} \right)\\ \Leftrightarrow 2m \le g\left( x \right)\,\,\forall x \in \left( { - 2; - 1} \right)\\ \Leftrightarrow 2m \le \mathop {\min }\limits_{\left[ { - 2; - 1} \right]} g\left( x \right)\end{array}\)
Xét hàm số \(g\left( x \right) = \dfrac{{3{x^2} + 1}}{x}\) \(\forall x \in \left( { - 2; - 1} \right)\).
\(g'\left( x \right) = \dfrac{{6x.x - 3{x^2} - 1}}{{{x^2}}} = \dfrac{{3{x^2} - 1}}{{{x^2}}}\), \(g'\left( x \right) = 0 \Leftrightarrow x = \pm \dfrac{1}{{\sqrt 3 }}\).
BBT:
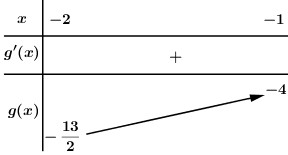
\( \Rightarrow 2m \le - \dfrac{{13}}{2} \Leftrightarrow m \le - \dfrac{{13}}{4}\).
Chọn C.


















