Phương pháp giải:

Lời giải chi tiết:

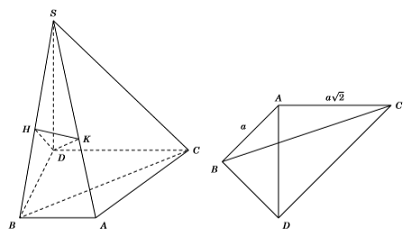
Gọi \(D\) là hình chiếu vuông góc của \(S\) lên mặt phẳng \(\left( {ABC} \right)\).

Ta có: \(\left\{ \begin{array}{l}AB \bot SB\,\,\left( {gt} \right)\\AB \bot SD\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {SBD} \right) \Rightarrow AB \bot BD\).

            \(\left\{ \begin{array}{l}AC \bot SA\,\,\left( {gt} \right)\\AC \bot SD\,\,\left( {SD \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow AC \bot \left( {SAD} \right) \Rightarrow AC \bot AD\).

Ta có:

\(\begin{array}{l}\angle BAC = \angle BAD + \angle DAC\\ \Rightarrow {135^0} = \angle BAD + {90^0}\\ \Rightarrow \angle BAD = {45^0}\end{array}\)

\( \Rightarrow \Delta ABD\) vuông cân tại \(B\) \( \Rightarrow AD = AB\sqrt 2  = a\sqrt 2  = AC\).

\( \Rightarrow \Delta ACD\) vuông cân tại \(A\).

Ta có: \(\angle BDC = \angle BDA + \angle ADC = {45^0} + {45^0} = {90^0} = \angle ABD\)

\( \Rightarrow ABDC\) là hình thang vuông tại \(B\) và \(D\).

Trong \(\left( {SBD} \right)\) kẻ \(DH \bot SB\,\,\left( {H \in SB} \right)\) ta có: \(\left\{ \begin{array}{l}DH \bot SB\\DH \bot AB\,\,\left( {AB \bot \left( {SBD} \right)} \right)\end{array} \right. \Rightarrow DH \bot \left( {SAB} \right)\).

Trong \(\left( {SAD} \right)\) kẻ \(DK \bot SA\,\,\left( {K \in SA} \right)\), ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}AC \bot AD\,\,\left( {cmt} \right)\\AC \bot SD\,\,\left( {SD \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow AC \bot \left( {SAD} \right) \Rightarrow AC \bot DK\\\left\{ \begin{array}{l}DK \bot SA\\DK \bot AC\end{array} \right. \Rightarrow DK \bot \left( {SAC} \right)\end{array}\).

\( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {DH;DK} \right) = \angle HDK = {30^0}\) (do \(DH \bot \left( {SAB} \right) \Rightarrow DH \bot HK \Rightarrow \Delta DHK\) vuông tại \(H\)).

Đặt \(SD = \,\,x > 0\).

Áp dụng hệ thức lượng trong tam giác vuông ta có:

\(\begin{array}{l}DH = \dfrac{{BD.SD}}{{\sqrt {B{D^2} + S{D^2}} }} = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }}\\DK = \dfrac{{AD.SD}}{{\sqrt {A{D^2} + S{D^2}} }} = \dfrac{{a\sqrt 2 .x}}{{\sqrt {2{a^2} + {x^2}} }} = \dfrac{{\sqrt 2 .ax}}{{\sqrt {2{a^2} + {x^2}} }}\end{array}\)

Xét tam giác vuông \(DHK\) có:

\(\begin{array}{l}\cos \angle HDK = \dfrac{{DH}}{{DK}}\\ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }}.\dfrac{{\sqrt {2{a^2} + {x^2}} }}{{\sqrt 2 .ax}}\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt {2{a^2} + {x^2}} }}{{\sqrt {2{a^2} + 2{x^2}} }}\\ \Leftrightarrow 6{a^2} + 6{x^2} = 8{a^2} + 4{x^2}\\ \Leftrightarrow 2{x^2} = 2{a^2} \Leftrightarrow x = a\end{array}\)

 Ta có \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC = \dfrac{1}{2}.a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}}}{2}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SD.{S_{\Delta ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\).

Chọn A.