Phương pháp giải:

- Tính độ dài các cạnh \(AC,\,\,BC\).

- Gọi \(G\) là trọng tâm \(\Delta ABC\) và \(M\) là trung điểm của \(AC\), áp dụng định lí Pytago tính \(BM\), từ đó suy ra độ dài \(BG\).

- Tiếp tục áp dụng định lí Pytago tính độ dài đường cao \(SG\).

- Sử dụng công thức tính thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}}\).

Lời giải chi tiết:

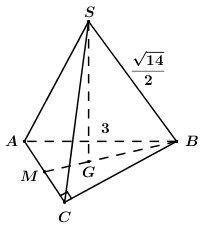
Do tam giác \(ABC\) vuông cân tại \(C\) có \(AB = 3\) nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{3}{{\sqrt 2 }}\).

Gọi \(G\) là trọng tâm \(\Delta ABC\) và \(M\) là trung điểm của \(AC\), khi đó ta có \(SG \bot \left( {ABC} \right)\) và \(AM = MC = \dfrac{1}{2}AC = \dfrac{3}{{2\sqrt 2 }}\).

Áp dụng định lí Pytago trong tam giác vuông \(BCM\) có:

\(BM = \sqrt {B{C^2} + C{M^2}}  = \sqrt {\dfrac{9}{2} + \dfrac{9}{8}}  = \sqrt {\dfrac{{45}}{8}}  = \dfrac{{3\sqrt {10} }}{4}\).

\( \Rightarrow GB = \dfrac{2}{3}BM = \dfrac{2}{3}.\dfrac{{3\sqrt {10} }}{4} = \dfrac{{\sqrt {10} }}{2}\).

Áp dụng định lý Pytago trong tam giác vuông \(SBG\) có:

\(SG = \sqrt {S{B^2} - B{G^2}}  = \sqrt {\dfrac{{14}}{4} - \dfrac{{10}}{4}}  = 1\).

Lại có: \({S_{\Delta ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}.\dfrac{3}{{\sqrt 2 }}.\dfrac{3}{{\sqrt 2 }} = \dfrac{9}{4}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}} = \dfrac{1}{3}.1.\dfrac{9}{4} = \dfrac{3}{4}\).

Chọn C.