Phương pháp giải:

Đặt các tỉ số $\dfrac{{AM}}{{AB}};\dfrac{{AN}}{{AD}}$ lần lượt là $x;y$.

Áp dụng tỉ số thể tích để tìm giá trị lớn nhất của $\dfrac{{{V_1}}}{V}$.

Lời giải chi tiết:

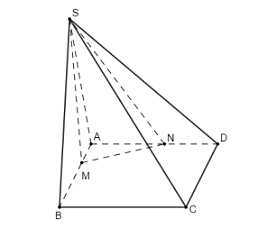
Đặt $\dfrac{{AM}}{{AB}} = x;\dfrac{{AN}}{{AD}} = y$

Theo giả thiết $2\dfrac{{AB}}{{AM}} + 3\dfrac{{AD}}{{AN}} = 8 \Rightarrow \dfrac{2}{x} + \dfrac{3}{y} = 8$

Áp dụng định lý Cosi ta có $\dfrac{2}{x} + \dfrac{3}{y} \ge 2\sqrt {\dfrac{6}{{xy}}}  \Rightarrow 8 \ge 2\sqrt {\dfrac{6}{{xy}}}  \Rightarrow xy \ge \dfrac{3}{8}$

Mặt khác $\dfrac{{{S_{AMN}}}}{{{S_{ABCD}}}} = \dfrac{1}{2}.\dfrac{{AM}}{{AB}}.\dfrac{{AN}}{{AD}} = \dfrac{{xy}}{2} \Rightarrow \dfrac{{{V_{SAMN}}}}{{{V_{SABC{\rm{D}}}}}} = \dfrac{{xy}}{2}$

$\Rightarrow \dfrac{{{V_1}}}{{{V_{SABC{\rm{D}}}}}} = 1 - \dfrac{{xy}}{2} \le \dfrac{{13}}{{16}}$ vì $xy \ge \dfrac{3}{8}$.

Dấu bằng xáy ra khi $\left\{ \begin{array}{l}\dfrac{2}{x} = \dfrac{3}{y}\\xy = \dfrac{3}{8}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{3}{4}\end{array} \right.$

Chọn A.