Phương pháp giải:

- Trong (ABC) kẻ $AH \bot BC\,\,\left( {H \in BC} \right)$, chứng minh $BC \bot \left( {OAH} \right)$ từ đó suy ra $OH \bot BC$.

- Sử dụng công thức Herong: $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$ để tính diện tích tam giác ABC.

- Tính AH dựa vào diện tích tam giác ABC.

- Sử dụng định lí Pytago để tính OH.

Lời giải chi tiết:

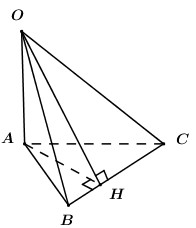
Trong (ABC) kẻ $AH \bot BC\,\,\left( {H \in BC} \right)$.

+ $\left\{ \begin{array}{l}BC \bot AH\\BC \bot OA\end{array} \right. \Rightarrow BC \bot \left( {OAH} \right) \Rightarrow BC \bot OH$.

$\Rightarrow {d_{\left[ {O;BC} \right]}} = OH$.

+ $\Delta ABC$: Nửa chu vi: $p = \dfrac{{7 + 5 + 8}}{2} = 10$.

                $\begin{array}{l}{S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - AC} \right)}  = 10\sqrt 3 \\{S_{\Delta ABC}} = \dfrac{1}{2}AH.BC \Rightarrow AH = \dfrac{{2{S_{ABC}}}}{{BC}} = 4\sqrt 3 \end{array}$

+ $\Delta OAH$: $OH = \sqrt {O{A^2} + A{H^2}}  = \sqrt {{4^2} + {{\left( {4\sqrt 3 } \right)}^2}}  = 8\,\,\left( {cm} \right)$.

Vậy ${d_{\left[ {O;BC} \right]}} = 8\,\,cm$.