Phương pháp giải:

- Phân chia và lắp ghép các khối đa diện.

- Muốn so sánh thể tích hai khối hình ta so sánh tỉ số chiều cao và tỉ số diện tích đáy của hai khối hình đó.

Lời giải chi tiết:

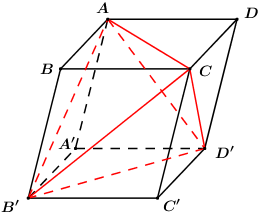
Đặt ${V_{ABCD.A'B'C'D'}} = V$.

Ta có: ${V_{ABCD.A'B'C'D'}} = {V_{ACB'D'}} + {V_{B'.ABC}} + {V_{D'.ACD}} + {V_{A.A'B'D'}} + {V_{C.B'C'D'}}$.

Ta có: ${V_{B'.ABC}} = \dfrac{1}{3}d\left( {B';\left( {ABC} \right)} \right).{S_{\Delta ABC}}$$= \dfrac{1}{3}d\left( {B';\left( {ABCD} \right)} \right).\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}V$.

Chứng minh tương tự ta có:  ${V_{D'.ACD}} = {V_{A.A'B'D'}} = {V_{C.B'C'D'}} = \dfrac{1}{6}V$.

 Khi đó ta có: $V = {V_{ACB'D'}} + 4.\dfrac{1}{6}V \Leftrightarrow {V_{ACB'D'}} = \dfrac{V}{3}$.

Vậy $\dfrac{{{V_{ACB'D'}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{V}{3}:V = \dfrac{1}{3}.$

Chọn D.