Câu hỏi:
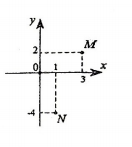
Gọi \(z,{\rm{w}}\) là các số phức có điểm biểu diễn lần lượt là \(M,\,\,N\) trên mặt phẳng Oxy như hình minh họa bên. Phần ảo của số phức \(\dfrac{z}{{\rm{w}}}\) là
- A \(\dfrac{{14}}{{17}}\)
- B \(3\)
- C \( - \dfrac{5}{{17}}\)
- D \( - \dfrac{1}{2}\)
Phương pháp giải:
- Từ đồ thị suy ra tọa độ của M, N.
- Tìm hai số phức z, w: Điểm \(M\left( {a;b} \right)\) biểu diễn cho số phức \(z = a + bi\).
- Tính \(\dfrac{z}{{\rm{w}}}\), sử dụng MTCT.
Lời giải chi tiết:
Dựa vào đồ thị ta có \(M\left( {3;2} \right),\)\(N\left( {1; - 4} \right).\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}z = 3 + 2i\\{\rm{w}} = 1 - 4i\end{array} \right.\\ \Rightarrow \dfrac{z}{{\rm{w}}} = \dfrac{{3 + 2i}}{{1 - 4i}} = - \dfrac{5}{{17}} + \dfrac{{14}}{{17}}i\end{array}\)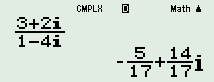
Khi đó phần ảo của số phức \(\dfrac{z}{{\rm{w}}}\) là \(\dfrac{{14}}{{17}}\)
Chọn A.


















