Phương pháp giải:

- Sử dụng các định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\), \(a \bot \left( P \right),\,\,a\parallel b \Rightarrow b \bot \left( P \right)\).

- Sử dụng khái niệm mặt phẳng trung trực: Mặt phẳng (P) được gọi là mặt phẳng trung trực của đoạn thẳng AB nếu mặt phẳng (P) đi qua trung điểm của AB và vuông góc với AB.

Lời giải chi tiết:

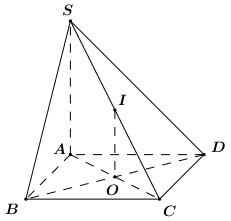
Vì IO là đường trung bình của tam giác SAC nên IO // SA. Mà \(SA \bot \left( {ABCD} \right)\) nên \(IO \bot \left( {ABCD} \right)\), do đó khẳng định A đúng.

Vì ABCD là hình vuông nên \(AC \bot BD\).

Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAC} \right)\) .

\(\left\{ \begin{array}{l}BD \bot \left( {SAC} \right)\\SC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow BD \bot SC\), do đó khẳng định B đúng.

Vì \(BD \bot \left( {SAC} \right)\,\,\left( {cmt} \right)\), (SAC) lại đi qua trung điểm O của BD, do đó (SAC) là mặt phẳng trung trực của BD, nên đáp án D đúng.

Vậy khẳng định C sai.

Chọn C.