Phương pháp giải:

- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường này và mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

- Sử dụng phương pháp đổi đỉnh, đổi về khoảng cách từ E đến $\left( {AC'B'} \right)$.

- Xác định khoảng cách và sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

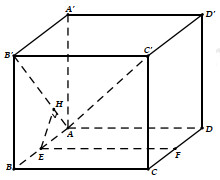
Ta có EF // B’C’ $\Rightarrow EF\parallel \left( {AC'B'} \right)$ $\Rightarrow d\left( {EF;AC'} \right) = d\left( {EF;\left( {AC'B'} \right)} \right) = d\left( {E;\left( {AC'B'} \right)} \right)$.

Kẻ $EH \bot AB'\,\,\left( {H \in AB'} \right)$.

Ta có: $C'B' \bot \left( {ABB'A'} \right) \Rightarrow B'C' \bot EH$ $\Rightarrow EH \bot \left( {AC'B'} \right)$.

$\Rightarrow d\left( {E;\left( {AC'B'} \right)} \right) = EH$.

Xét tam giác AEH vuông cân tại H có: $EA = \dfrac{a}{2} \Rightarrow EH = \dfrac{{a\sqrt 2 }}{4}$.

Vậy $d\left( {EF;AC'} \right) = \dfrac{{a\sqrt 2 }}{4}.$

Chọn B.