Câu hỏi:
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc, \(OA = OB = a\), \(OC = 2a\). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(OM\) và \(AC\) bằng:
- A \(\dfrac{{2\sqrt 5 a}}{5}\)
- B \(\dfrac{{a\sqrt 2 }}{2}\)
- C \(\dfrac{{a\sqrt 2 }}{3}\)
- D \(\dfrac{{2a}}{3}\)
Phương pháp giải:
- Gọi \(D\) là điểm đối xứng với \(B\) qua \(O\). Chứng minh \(d\left( {OM;AC} \right) = d\left( {O;\left( {ACD} \right)} \right)\).
- Sử dụng công thức giải nhanh: Tứ giác \(OACD\) có \(OA,\,\,OC,\,\,OD\) đôi một vuông góc nên \(\dfrac{1}{{{d^2}\left( {O;\left( {ACD} \right)} \right)}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}}\).
Lời giải chi tiết:
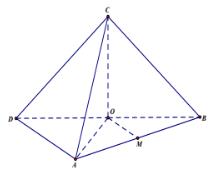
Gọi \(D\) là điểm đối xứng với \(B\) qua \(O\).
Ta có: \(OM\) là đường trung bình của tam giác \(ABD\) nên \(OM\parallel AD \Rightarrow OM\parallel \left( {ACD} \right)\).
\( \Rightarrow d\left( {OM;AC} \right) = d\left( {OM;\left( {ACD} \right)} \right) = d\left( {O;\left( {ACD} \right)} \right)\).
Vì tứ giác \(OACD\) có \(OA,\,\,OC,\,\,OD\) đôi một vuông góc nên \(\dfrac{1}{{{d^2}\left( {O;\left( {ACD} \right)} \right)}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} = \dfrac{9}{{4{a^2}}}\).
\( \Rightarrow d\left( {O;\left( {ACD} \right)} \right) = \dfrac{{2a}}{3}\).
Vậy \(d\left( {OM;AC} \right) = \dfrac{{2a}}{3}\).
Chọn D.


















