Câu hỏi:
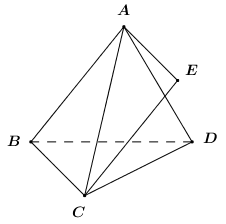
Cho tứ diện đều \(ABCD\). Tính góc giữa hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \).
- A \(30^\circ \).
- B \(90^\circ \).
- C \(120^\circ \).
- D \(60^\circ \).
Phương pháp giải:
- Dựng vectơ gốc \(A\) bằng vectơ \(\overrightarrow {BC} \).
- Chứng minh \(\Delta ABC\) đều, sử dụng tính chất của tam giác đều.
Lời giải chi tiết:
Dựng hình bình hành \(ABCE\), khi đó ta có \(\overrightarrow {BC} = \overrightarrow {AE} \).
\( \Rightarrow \angle \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = \angle \left( {\overrightarrow {AB} ;\overrightarrow {AE} } \right) = \angle BAE\).
Vì tứ diện \(ABCD\) đều nên \(AB = BC = CA \Rightarrow \Delta ABC\) đều.
Do đó \(\angle ABC = {60^0}\).
Mà \(ABCE\) là hình bình hành (theo cách dựng) nên \(\angle BAE = {180^0} - \angle ABC = {120^0}\).
Vậy \(\angle \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = {120^0}\).
Chọn C.