Phương pháp giải:

- Xác định quỹ tích các điểm biểu diễn số phức \(\overline z \), sử dụng các công thức \(\left| z \right| = \left| {\overline z } \right|,\,\,\overline {z + w}  = \overline z  + \overline w \).

- Biểu diễn hình học và tìm GTLN, GTNN của \(\left| {\overline z  + 1 + i} \right|\).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\left| {iz - 2i + 1} \right| = 1 \Leftrightarrow \left| {iz - 2i - {i^2}} \right| = 1\\ \Leftrightarrow \left| {i\left( {z - 2 - i} \right)} \right| = 1 \Leftrightarrow \left| i \right|\left| {z - 2 - i} \right| = 1\end{array}\)

\(\begin{array}{l} \Rightarrow \left| {z - 2 - i} \right| = 1 \Rightarrow \left| {\overline {z - 2 - i} } \right| = 1\\ \Leftrightarrow \left| {\overline z  + \overline { - 2 - i} } \right| = 1 \Leftrightarrow \left| {\overline z  - 2 + i} \right| = 1 \Leftrightarrow \left| {\overline z  - \left( {2 - i} \right)} \right| = 1\end{array}\).

Suy ra tập hợp các điểm biểu diễn số phức \(\overline z \) là tâm đường tròn \(\left( C \right)\) tâm \(I\left( {2; - 1} \right)\), bán kính \(R = 1\).

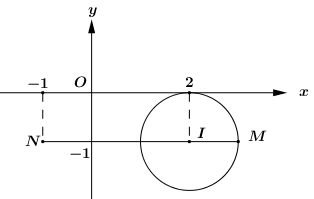
Gọi \(M\) là điểm biểu diễn số phức \(\overline z \), \(N\left( { - 1; - 1} \right)\) là điểm biểu diễn số phức \(z =  - 1 - i\).

Khi đó ta có: \(\left| {\overline z  + 1 + i} \right| = \left| {\overline z  - \left( { - 1 - i} \right)} \right| = MN\) với \(M \in \left( C \right)\).

Ta có: \(\left\{ \begin{array}{l}M{N_{\min }} = IN - R = 3 - 1 = 2\\M{N_{\max }} = IN + R = 3 + 1 = 4\end{array} \right.\) \( \Rightarrow m = 2,\,\,M = 4\).

Vậy \(M + m = 4 + 2 = 6\).

Chọn C.