Câu hỏi:
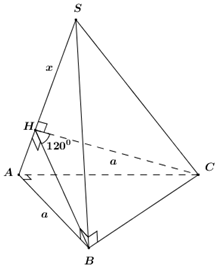
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\), \(\angle SBA = \angle SCA = {90^0}\), góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) bằng \({60^0}\). Thể tích khối chóp đã cho bằng:
- A \({a^3}\)
- B \(\dfrac{{{a^3}}}{3}\)
- C \(\dfrac{{{a^3}}}{2}\)
- D \(\dfrac{{{a^3}}}{6}\)
Phương pháp giải:
- Kẻ \(BH \bot SA\), chứng minh \(CH \bot SA\).
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Chứng minh \(\angle BHC = {120^0}\).
- Đặt \(SH = x\), sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tìm \(x\) theo \(a\).
- Chứng minh \(SH \bot \left( {BHC} \right)\), từ đó suy ra \({V_{ABCD}} = \dfrac{1}{3}{S_{BCH}}.SA\).
Lời giải chi tiết:
Dễ dàng chứng minh được \(\Delta SAB = \Delta SAC\) (2 cạnh góc vuông).
Trong \(\left( {SAB} \right)\) kẻ \(BH \bot SA\) \(\left( {H \in SA} \right)\).
Xét \(\Delta ABH\) và \(\Delta ACH\) có:
\(\begin{array}{l}AB = AC\,\,\,\left( {gt} \right)\\AH\,\,chung\\\angle HAB = \angle HAC\,\,\left( {do\,\,\Delta SAB = \Delta SAC} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow \Delta ABH = \Delta ACH\,\,\left( {c.g.c} \right)\\ \Rightarrow \angle AHB = \angle AHC = {90^0},\,\,BH = CH\end{array}\)
Do đó \(CH \bot SA\) tại \(H\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAC} \right) = SA\\\left( {SAB} \right) \supset BH \bot SA\\\left( {SAC} \right) \supset CH \bot SA\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SAC} \right)} \right) = \angle \left( {BH;CH} \right) = {60^0}\).
\( \Rightarrow \angle BHC = {60^0}\) hoặc \(\angle BHC = {120^0}\).
Nếu \(\angle BHC = {60^0}\)\( \Rightarrow \Delta BCH\) đều cạnh \(BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt 2 \).
\( \Rightarrow BH = a\sqrt 2 > AB\) (mâu thuẫn do \(BH\) là đường vuông góc, \(AB\) là đường xiên).
Suy ra \(\angle BHC = {120^0}\).
Áp dụng định lí Cosin trong tam giác \(BCH\) ta có:
\(\begin{array}{l}B{H^2} + C{H^2} - B{C^2} = 2BH.CH.\cos {120^0}\\ \Rightarrow 2B{H^2} - 2{a^2} = 2B{H^2}.\dfrac{{ - 1}}{2}\\ \Leftrightarrow 3B{H^2} = 2{a^2} \Leftrightarrow BH = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }} = CH\end{array}\)
Áp dụng định lí Pytago trong tam giác vuông \(ABH\) ta có:
\(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - \dfrac{{2{a^2}}}{3}} = \dfrac{a}{{\sqrt 3 }}\)
Đặt \(SH = x\,\,\left( {x > 0} \right) \Rightarrow SA = x + \dfrac{a}{{\sqrt 3 }}\).
Áp dụng định lí Pytago trong tam giác vuông \(SBH\) ta có:
\(SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {{x^2} + \dfrac{{2{a^2}}}{3}} \).
Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có:
\(\begin{array}{l}SB.AB = BH.SA\\ \Leftrightarrow \sqrt {{x^2} + \dfrac{{2{a^2}}}{3}} .a = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}.\left( {x + \dfrac{a}{{\sqrt 3 }}} \right)\\ \Leftrightarrow \sqrt {{x^2} + \dfrac{{2{a^2}}}{3}} = \dfrac{{\sqrt 2 }}{{\sqrt 3 }}.\left( {x + \dfrac{a}{{\sqrt 3 }}} \right)\\ \Leftrightarrow {x^2} + \dfrac{{2{a^2}}}{3} = \dfrac{2}{3}{\left( {x + \dfrac{a}{{\sqrt 3 }}} \right)^2}\\ \Leftrightarrow {x^2} + \dfrac{{2{a^2}}}{3} = \dfrac{2}{3}{x^2} + \dfrac{{4ax}}{{3\sqrt 3 }} + \dfrac{{2{a^2}}}{9}\\ \Leftrightarrow \dfrac{{4{a^2}}}{9} - \dfrac{{4ax}}{{\sqrt 3 }} + \dfrac{1}{3}{x^2} = 0\\ \Leftrightarrow {\left( {\dfrac{2}{3}a - \dfrac{x}{{\sqrt 3 }}} \right)^2} = 0\\ \Leftrightarrow \dfrac{2}{3}a - \dfrac{x}{{\sqrt 3 }} = 0 \Leftrightarrow x = \dfrac{2}{{\sqrt 3 }}a\\ \Rightarrow SA = x + \dfrac{a}{{\sqrt 3 }} = \dfrac{{2a}}{{\sqrt 3 }} + \dfrac{a}{{\sqrt 3 }} = a\sqrt 3 \end{array}\)
Ta có: \(\left\{ \begin{array}{l}SA \bot BH\\SA \bot CH\end{array} \right. \Rightarrow SA \bot \left( {BCH} \right)\).
Và \({S_{BCH}} = \dfrac{1}{2}BH.CH.\sin \angle BHC = \dfrac{1}{2}.{\left( {\dfrac{{a\sqrt 2 }}{{\sqrt 3 }}} \right)^2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{6}\).
\(\begin{array}{l} \Rightarrow {V_{ABCD}} = \dfrac{1}{3}SH.{S_{BCH}} + \dfrac{1}{3}AH.{S_{BCH}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}{S_{BCH}}.\left( {SH + AH} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}{S_{BCH}}.SA\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{6}.a\sqrt 3 = \dfrac{{{a^3}}}{6}\end{array}\)
Chọn D.