Câu hỏi:
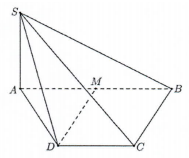
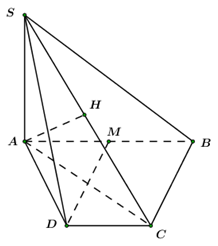
Cho hình chóp \(SABCD\) có đáy là hình thang, \(AB = 2a,\) \(AD = DC = CB = a,\)\(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB.\) Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng:
- A \(\dfrac{{3a}}{4}\)
- B \(\dfrac{{3a}}{2}\)
- C \(\dfrac{{3\sqrt {13} a}}{{13}}\)
- D \(\dfrac{{6\sqrt {13} a}}{{13}}\)
Phương pháp giải:
- Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách từ đường thẳng này đến mặt phẳng song song với đường thẳng này và chứa đường thẳng kia.
- Đổi về khoảng cách từ đỉnh A.
- Chứng minh \(BC \bot \left( {SAC} \right)\), từ đó dựng khoảng cách từ \(A\) đến \(\left( {SBC} \right).\)
- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
Vì \(\left\{ \begin{array}{l}CD = BM = a\\CD\parallel BM\end{array} \right.\,\,\left( {gt} \right)\) nên \(BCDM\) là hình bình hành (dhnb).
\( \Rightarrow DM\parallel BC\) (2 cạnh đối của hình bình hành).
Mà \(BC \subset \left( {SCD} \right)\) \( \Rightarrow DM\parallel \left( {SBC} \right) \supset SB\).
\( \Rightarrow d\left( {SB;DM} \right) = d\left( {DM;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right)\).
Ta có: \(AM \cap \left( {SBC} \right) = B \Rightarrow \dfrac{{d\left( {M;\left( {SBC} \right)} \right)}}{{d\left( {A;\left( {SBC} \right)} \right)}} = \dfrac{{MB}}{{AB}} = \dfrac{1}{2}\).
\( \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right)\).
Chứng minh tương tự ta có: \(ADCM\) là hình bình hành .
Khi đó ta có \(CM = \dfrac{1}{2}AB\,\,\left( { = a} \right)\), do đó \(\Delta ACB\) vuông tại \(C\) (định lí đường trung tuyến trong tam giác).
\( \Rightarrow AC \bot BC\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAC} \right)\).
Trong \(SAC\) kẻ \(AH \bot SC\,\,\left( {H \in SC} \right)\) ta có:
\(\left\{ \begin{array}{l}AH \bot BC\,\,\,\left( {BC \bot \left( {SAC} \right)} \right)\\AH \bot SC\end{array} \right.\) \( \Rightarrow AH \bot \left( {SBC} \right)\) \( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH\) \( \Rightarrow d\left( {DM;SB} \right) = \dfrac{1}{2}AH\).
Áp dụng định lí Pytago trong tam giác vuông \(ACD\) ta có:
\(AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \).
Áp dụng hệ thức lượng trong tam giác vuông \(SAC\,\,\left( {SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC} \right)\) ta có:
\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{9{a^2}}}\\ \Rightarrow AH = \dfrac{{3a}}{2}\end{array}\)
Vậy \(d\left( {DM;SB} \right) = \dfrac{1}{2}AH = \dfrac{{3a}}{4}\).
Chọn A.