Phương pháp giải:

Tập tỉ lệ thể tích của khối $A'.BCO$ và khối lăng trụ $ABCD.A'B'C'D'$ dựa vào tỉ lệ chiều cao và tỉ lệ diện tích đáy tương ứng.

Lời giải chi tiết:

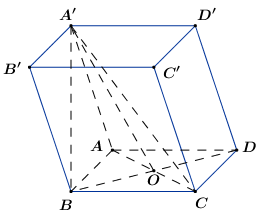
Ta có: ${S_{BCO}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{4}{S_{ABCD}}$ $\Rightarrow {V_{A'.BCO}} = \dfrac{1}{4}{V_{A'.ABCD}}.$

Mà ${V_{A'.ABCD}} = \dfrac{1}{3}{V_{ABCD.A'B'C'D'}}$ (thể tích chóp và lăng trụ có cùng chiều cao và diện tích đáy).

$\Rightarrow {V_{A'.BCO}} = \dfrac{1}{4}.\dfrac{1}{3}.{V_{ABCD.A'B'C'D'}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1.$

Chọn B.