Câu hỏi:
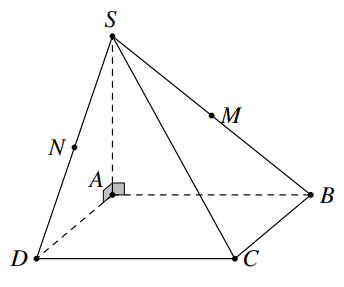
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 3 \). Gọi \(M,\,\,N\) lần lượt là trung điểm của cạnh \(SB\) và \(SD\); mặt phẳng \(\left( {AMN} \right)\) cắt \(SC\) tại \(I\). Tính thể tích khối đa diện \(ABCDMNI\).
- A \(\dfrac{{5\sqrt 3 {a^3}}}{{18}}\)
- B \(\dfrac{{5\sqrt 3 {a^3}}}{6}\)
- C \(\dfrac{{13\sqrt 3 {a^3}}}{{36}}\)
- D \(\dfrac{{\sqrt 3 {a^3}}}{{18}}\)
Phương pháp giải:
- Tính tỉ số \(\dfrac{{SI}}{{SC}}\).
- Sử dụng công thức tỉ số thể tích: Cho tứ diện\(S.ABC\). Các điểm \(M,N,P\) lần lượt nằm trên các cạnh \(SA,\,\,SB,\,\,SC\) thì \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}.\)
- Tính tỉ số thể tích \(\dfrac{{{V_{S.ANMI}}}}{{{V_{S.ABCD}}}}\) để tính thể tích khối \(ABCDMNI\).
Lời giải chi tiết:
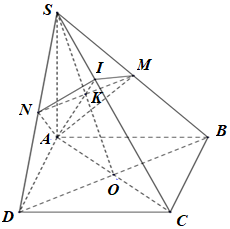
Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Trong mặt phẳng \(\left( {SBD} \right),\) gọi \(K = SO \cap MN\).
Trong mặt phẳng \(\left( {SAC} \right),\) gọi \(I = AK \cap SC\), suy ra \(I\) chính là giao điểm của \(SC\) và \(mp\left( {AMN} \right)\).
Ta có:
\(MN\) là đường trung bình trong tam giác \(SBD\), suy ra \(\left\{ \begin{array}{l}MN\parallel BD\\MN = \dfrac{1}{2}BD\end{array} \right.\)
\( \Rightarrow NK\parallel DO \Rightarrow \dfrac{{SK}}{{SO}} = \dfrac{{SN}}{{SD}} = \dfrac{1}{2}.\)
Áp dụng định lí Menelaus vào tam giác \(SOC\) có cát tuyến \(AKI\):
\(\dfrac{{SI}}{{IC}}.\dfrac{{AC}}{{AO}}.\dfrac{{KO}}{{KS}} = 1 \Leftrightarrow \dfrac{{SI}}{{IC}}.2.1 = 1\)\( \Rightarrow \dfrac{{SI}}{{IC}} = \dfrac{1}{2} \Rightarrow \dfrac{{SI}}{{SC}} = \dfrac{1}{3}\)
Ta có:
\(\begin{array}{l}\dfrac{{{V_{S.ANI}}}}{{{V_{S.ADC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SN}}{{SD}}.\dfrac{{SI}}{{SC}} = 1.\dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\\ \Rightarrow {V_{S.ANI}} = \dfrac{1}{6}{V_{S.ADC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\\dfrac{{{V_{S.AIM}}}}{{{V_{S.ACB}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SI}}{{SC}}.\dfrac{{SM}}{{SB}} = 1.\dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6}\\ \Rightarrow {V_{S.AIM}} = \dfrac{1}{6}{V_{S.ADC}} = \dfrac{1}{{12}}{V_{S.ABCD}}\\ \Rightarrow {V_{S.ANIM}} = {V_{S.ANI}} + {V_{AIM}} = \dfrac{1}{{12}}{V_{S.ABCD}} + \dfrac{1}{{12}}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}}\\ \Rightarrow {V_{ABCDMNI}} = {V_{S.ABCD}} - {V_{S.ANIM}} = \dfrac{5}{6}{V_{S.ABCD}}.\end{array}\)
Thể tích của khối chóp \(S.ABCD\)là: \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} = \dfrac{{\sqrt 3 {a^3}}}{3}.\)
Vậy thể tích của khối đa diện \(ABCDMNI\) là: \({V_{ABCDMNI}} = \dfrac{5}{6}{V_{S.ABCD}} = \dfrac{{5\sqrt 3 {a^3}}}{{18}}.\)
Chọn A.


















