Câu hỏi:
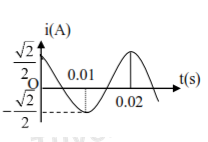
Đồ thị hình bên mô tả sự biến thiên của cường độ dòng điện xoay chiều theo thời gian. Biểu thức của cường độ dòng điện tức thời có biểu thức
- A \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A.\)
- B \(i = 2cos\left( {100\pi t} \right)A.\)
- C \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A.\)
- D \(i = 1cos\left( {100\pi t} \right)A.\)
Phương pháp giải:
+ Đọc đồ thị i-t
+ Sử dụng biểu thức \(\omega = \dfrac{{2\pi }}{T}\)
+ Viết phương trình cường độ dòng điện
Lời giải chi tiết:
Từ đồ thị ta có:
+ Cường độ dòng điện cực đại: \({I_0} = \dfrac{{\sqrt 2 }}{2}A\)
+ Chu kì dao động: \(T = 0,02s\)
\( \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,02}} = 100\pi \)
+ Tại thời điểm ban đầu, dòng điện có giá trị cực đại: \( \Rightarrow {i_0} = {I_0}cos\varphi = {I_0} \Rightarrow cos\varphi = 1 \Rightarrow \varphi = 0\)
\( \Rightarrow \) Phương trình cường độ dòng điện: \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A\)
Chọn C