Phương pháp giải:

Tần số góc của sóng: $\omega  = 2\pi f$

Biên độ dao động của điểm cách bụng sóng khoảng y: ${A_M} = {A_{bung}}.\left| {\cos \dfrac{{2\pi y}}{\lambda }} \right|$

Tỉ số li độ giữa hai điểm, một điểm nằm trên bó chẵn, một điểm nằm trên bó lẻ: $\dfrac{{{u_M}}}{{{u_N}}} =  - \dfrac{{{A_M}}}{{{A_N}}}$

Công thức độc lập với thời gian:

$\left\{ \begin{array}{l}{u_M}^2 + \dfrac{{{v_M}^2}}{{{\omega ^2}}} = {A_M}^2\\{a_N} = \left| {{\omega ^2}.{u_N}} \right|\end{array} \right.$

Lời giải chi tiết:

Tần số góc của sóng: $\omega  = 2\pi f = 2\pi .10 = 20\pi \,\,\left( {rad/s} \right)$

Điểm M thuộc bụng sóng có biên độ dao động: ${A_M} = {A_{bung}} = 6\,\,\left( {mm} \right)$

Biên độ dao động của điểm N là:

${A_M} = {A_{bung}}.\left| {\cos \dfrac{{2\pi y}}{\lambda }} \right| = 6.\left| {\cos \dfrac{{2\pi .8}}{6}} \right| = 3\,\,\left( {mm} \right)$

Ở thời điểm t, xét điểm M, ta có công thức độc lập với thời gian:

$\begin{array}{l}{u_M}^2 + \dfrac{{{v_M}^2}}{{{\omega ^2}}} = {A_M}^2 \Rightarrow {u_M}^2 + \dfrac{{{{\left( {6\pi } \right)}^2}}}{{{{\left( {20\pi } \right)}^2}}} = 0,{6^2}\\ \Rightarrow {u_M} =  \pm 0,3\sqrt 3 \,\,\left( {cm} \right)\end{array}$

Ta có hình vẽ:

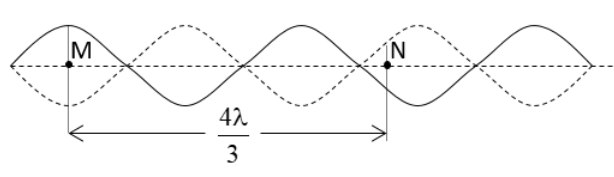
Nhận xét: điểm N nằm trên bó sóng chẵn, điểm M nằm trên bó lẻ

Tỉ số giữa li độ hai điểm M, N là:

$\begin{array}{l}\dfrac{{{u_M}}}{{{u_N}}} =  - \dfrac{{{A_M}}}{{{A_N}}} \Rightarrow {u_N} =  - \dfrac{{{A_N}}}{{{A_M}}}.{u_M}\\ \Rightarrow {u_N} =  - \dfrac{3}{6}.\left( { \pm 0,3\sqrt 3 } \right) =  \mp 0,3\dfrac{{\sqrt 3 }}{2}\,\,\left( {cm} \right)\end{array}$

Độ lớn gia tốc của điểm N tại thời điểm t là:

$\begin{array}{l}{a_N} = \left| {{\omega ^2}.{u_N}} \right| = \left| {{{\left( {20\pi } \right)}^2}.\left( { \mp 0,3.\dfrac{{\sqrt 3 }}{2}} \right)} \right|\\ \Rightarrow {a_N} = 600\sqrt 3 \,\,\left( {cm/{s^2}} \right) = 6\sqrt 3 \,\,\left( {m/{s^2}} \right)\end{array}$

Chọn A.