Phương pháp giải:

Lời giải chi tiết:

Gọi \(a,\,\,b,\,\,c,\,\,d\)  lần lượt là khoảng cách từ \(O\) đến các mặt phẳng \(\left( {SAB} \right)\), \(\left( {SBC} \right)\), \(\left( {SCD} \right)\), \(\left( {SDA} \right)\).

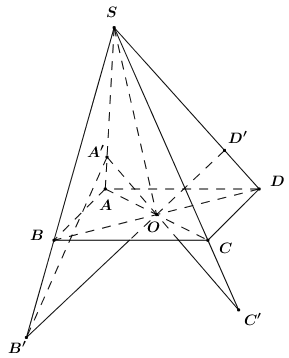
Trong mặt phẳng \(\left( {SAC} \right)\) dựng đường thẳng đi qua \(O\) vuông góc với \(SO\) cắt 2 đường thẳng  \(SA,\,\,SC\) lần lượt tại \(A',\,\,C'\).

Trong mặt phẳng .. dựng đường thẳng đi qua \(O\) vuông góc với \(SO\) cắt 2 đường thẳng \(SB,\,\,SD\) lần lượt tại \(B',\,\,D'\).

Ta có\(\left\{ \begin{array}{l}\left( {SAC} \right) \bot \left( {SBD} \right)\\\left( {SAC} \right) \cap \left( {SBD} \right) = SO\\\left( {SAC} \right) \supset A'C' \bot SO\end{array} \right.\)\( \Rightarrow A'C' \bot \left( {SBD} \right) \Rightarrow A'C' \bot B'D',\,\,A'C' \bot SO.\)

Khi đó, khối tứ diện \(OA'B'S\) có \(OA',\,\,OB',\,\,OS\) đôi một vuông góc nên ta có:

\(\dfrac{1}{{{a^2}}} = \dfrac{1}{{A'{O^2}}} + \dfrac{1}{{B'{O^2}}} + \dfrac{1}{{S{O^2}}}\,\,\,\left( 1 \right)\)

Chứng minh tương tự ta có:

\(\begin{array}{l}\dfrac{1}{{{b^2}}} = \dfrac{1}{{B'{O^2}}} + \dfrac{1}{{C'{O^2}}} + \dfrac{1}{{S{O^2}}}\,\,\,\,\,\left( 2 \right)\\\dfrac{1}{{{c^2}}} = \dfrac{1}{{C'{O^2}}} + \dfrac{1}{{D'{O^2}}} + \dfrac{1}{{S{O^2}}}\,\,\,\,\,\left( 3 \right)\\\dfrac{1}{{{d^2}}} = \dfrac{1}{{D'{O^2}}} + \dfrac{1}{{A'{O^2}}} + \dfrac{1}{{S{O^2}}}\,\,\,\,\,\left( 4 \right)\end{array}\)

Từ (1), (2), (3), (4) suy ra: \(\dfrac{1}{{{a^2}}} + \dfrac{1}{{{c^2}}} = \dfrac{1}{{{b^2}}} + \dfrac{1}{{{d^2}}}\)

Theo bài ra ta có: \(a = 1,\,\,b = \dfrac{1}{2},\,\,c = \dfrac{1}{3}\),

\(\begin{array}{l} \Rightarrow \dfrac{1}{{{1^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{3}} \right)}^2}}} = \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^2}}} + \dfrac{1}{{{d^2}}}\\ \Rightarrow d = \dfrac{1}{{\sqrt 6 }} \Rightarrow d\left( {O;\left( {SDA} \right)} \right) = \dfrac{1}{{\sqrt 6 }}\end{array}\)

Gọi \(V = {V_{S.ABCD}}\)

Ta có: \(\left\{ \begin{array}{l}{S_{OAB}} = {S_{OBC}} = {S_{OCD}} = {S_{ODA}} = \dfrac{1}{4}{S_{ABCD}}\\d\left( {S;\left( {OAB} \right)} \right) = \left( {S;\left( {OBC} \right)} \right) = \left( {S;\left( {OCD} \right)} \right) = \left( {S;\left( {ODA} \right)} \right) = \left( {S;\left( {ABCD} \right)} \right)\end{array} \right.\)

\( \Rightarrow {V_{S.OAB}} = {V_{S.OBC}} = {V_{S.OCD}} = {V_{S.ODA}} = \dfrac{1}{4}{V_{S.ABCD}} = \dfrac{1}{4}V\)

Lại có:

\(\begin{array}{l}\dfrac{1}{4}V = {V_{S.OAB}} = \dfrac{1}{3}d\left( {O;\left( {SAB} \right)} \right).{S_{SAB}} = \dfrac{1}{3}.1.{S_{SAB}} \Rightarrow {S_{SAB}} = \dfrac{3}{4}V\,\,\,\,\,\,\,\,\,\,\,\,\left( 5 \right)\\\dfrac{1}{4}V = {V_{S.OBC}} = \dfrac{1}{3}d\left( {O;\left( {SBC} \right)} \right).{S_{SBC}} = \dfrac{1}{3}.\dfrac{1}{2}.{S_{SBC}} \Rightarrow {S_{SBC}} = \dfrac{3}{2}V\,\,\,\,\,\,\,\,\,\left( 6 \right)\\\dfrac{1}{4}V = {V_{S.OCD}} = \dfrac{1}{3}d\left( {O;\left( {SCD} \right)} \right).{S_{SCD}} = \dfrac{1}{3}.\dfrac{1}{3}.{S_{SCD}} \Rightarrow {S_{SCD}} = \dfrac{9}{4}V\,\,\,\,\,\,\,\,\left( 7 \right)\\\dfrac{1}{4}V = {V_{S.OAD}} = \dfrac{1}{3}\left( {O;\left( {SDA} \right)} \right).{S_{SAD}} = \dfrac{1}{3}.\dfrac{1}{{\sqrt 6 }}.{S_{SAD}} \Rightarrow {S_{SAD}} = \dfrac{{3\sqrt 6 }}{4}V\,\,\,\left( 8 \right)\end{array}\)

Cộng (5), (6), (7), (8) vế theo vế ta được:

\(\begin{array}{l}{S_{SAB}} + {S_{SBC}} + {S_{SCD}} + {S_{SAD}} = \dfrac{3}{4}V + \dfrac{3}{2}V + \dfrac{9}{4}V + \dfrac{{3\sqrt 6 }}{4}V\\ \Leftrightarrow 6 + \sqrt 6  = \dfrac{3}{4}\left( {6 + \sqrt 6 } \right)V\\ \Leftrightarrow V = \dfrac{4}{3}\end{array}\)

Vậy \({V_{S.ABCD}} = \dfrac{4}{3}\).

Chọn D.