Phương pháp giải:

Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\), chứng minh \(OA = OB = OC = OM = ON\).

Lời giải chi tiết:

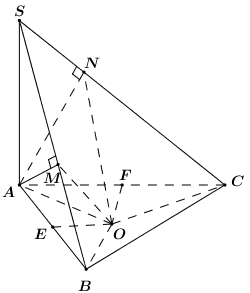
Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,AC\) và \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Tam giác \(ABM\) vuông tại \(M\) nên \(E\) là tâm đường tròn ngoại tiếp tam giác \(ABM\).

Ta có: \(\left\{ \begin{array}{l}OE \bot AB\\OE \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow OE \bot \left( {SAB} \right)\) \( \Rightarrow OE \bot \left( {ABM} \right)\).

Do đó \(OA = OB = OM\).

Chứng minh tương tự ta có \(OA = OC = ON\).

Lại có \(OA = OB = OC\) nên \(OA = OB = OC = OM = ON\).

Do đó \(O\) chính là tâm mặt cầu ngoại tiếp đa diện \(ABCNM\), và bán kính mặt cầu là \(R = OA\), cũng chính là bán kính đường tròn ngoại tiếp tam giác \(ABC\).

Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC\) \( = \dfrac{1}{2}.3.2.\sin {60^0} = \dfrac{{3\sqrt 3 }}{2}\).

Áp dụng định lí cosin trong tam giác giác \(ABC\) ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \angle BAC\\B{C^2} = {3^2} + {2^2} - 2.3.2.\cos {60^0}\\B{C^2} = 7\\ \Rightarrow BC = \sqrt 7 \end{array}\)

Vậy \(R = OA = \dfrac{{AB.BC.AC}}{{4{S_{\Delta ABC}}}}\) \( = \dfrac{{3.2.\sqrt 7 }}{{4.\dfrac{{3\sqrt 3 }}{2}}} = \dfrac{{\sqrt {21} }}{3}\).

Chọn B.