Phương pháp giải:

Lời giải chi tiết:

Xét tam giác $ABD$ có: $\left\{ \begin{array}{l}AB = AD\\\angle BAD = {60^0}\end{array} \right.$ $\Rightarrow \Delta ABD$ đều.

Gọi $H$ là trọng tâm $\Delta ABD$, do $SA = SB = SD$ nên $SH \bot \left( {ABCD} \right)$.

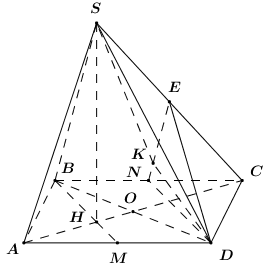
Gọi $M$ là trung điểm của $AD$, ta có $BM \bot AD \Rightarrow BM \bot BC$.

Ta có: $\left\{ \begin{array}{l}BC \bot BM\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SBM} \right)$.

Goi $N,\,\,E$ lần lượt là trung điểm của $BC$ và $SC$ ta có:

$\left\{ \begin{array}{l}BN\parallel DM\\BN = DM\end{array} \right. \Rightarrow BNDM$ là hình bình hành $\Rightarrow DN\parallel BM$.

Lại có $NE$ là đường trung bình của tam giác $SBC$ nên $NE\parallel SB$.

$\Rightarrow \left( {NDE} \right)\parallel \left( {SBM} \right)$.

Mà $BC \bot \left( {SBM} \right)$ nên $BC \bot \left( {NDE} \right)$.

Trong $\left( {NDE} \right)$ kẻ $DK \bot NE\,\,\,\left( {K \in NE} \right)$ ta có:

$\left\{ \begin{array}{l}DK \bot NE\\DK \bot BC\,\,\left( {BC \bot \left( {NDE} \right)} \right)\end{array} \right.$$\Rightarrow DK \bot \left( {SBC} \right)$.

$\Rightarrow$ Hình chiếu của $SD$ lên $\left( {SBC} \right)$ là $SK$.

$\Rightarrow \angle \left( {SD;\left( {SBC} \right)} \right) = \angle \left( {SD;SK} \right) = \angle DSK$.

Xét tam giác $SHA$ có $AH = \dfrac{2}{3}AO = \dfrac{{a\sqrt 3 }}{3}$, $SA = \dfrac{{a\sqrt 3 }}{2}$.

Áp dụng định lí Pytago ta có: $SH = \sqrt {S{A^2} - A{H^2}}  = \dfrac{{a\sqrt {15} }}{6}$.

Ta có: $AC = 2AO = a\sqrt 3$ $\Rightarrow HC = AC - AH = \dfrac{{2a\sqrt 3 }}{3}$.

Áp dụng định lí Pytago trong tam giác vuông $SHC$ ta có: $SC = \sqrt {S{H^2} + H{C^2}}  = \dfrac{{a\sqrt 7 }}{2}$.

Xét tam giác $SCD$ có:

$\begin{array}{l}D{E^2} = \dfrac{{S{D^2} + C{D^2}}}{2} - \dfrac{{S{C^2}}}{4}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{3{a^2}}}{4} + {a^2}}}{2} - \dfrac{{7{a^2}}}{{16}}\\ \Rightarrow DE = \dfrac{{a\sqrt 7 }}{4}\end{array}$

Xét tam giác $DNE$ ta có: $DN = BM = \dfrac{{a\sqrt 3 }}{2}$, $NE = \dfrac{1}{2}SB = \dfrac{{a\sqrt 3 }}{4}$, $DE = \dfrac{{a\sqrt 7 }}{4}$.

Gọi $p$ là nửa chu vi tam giác $DNE$ ta có: $p = \dfrac{{\sqrt 7  + 3\sqrt 3 }}{8}$.

Diện tích tam giác $DNE$ là: ${S_{DNE}} = \sqrt {p\left( {p - DN} \right)\left( {p - DE} \right)\left( {p - NE} \right)}  = \dfrac{{{a^2}\sqrt 5 }}{{16}}$.

Lại có ${S_{DNE}} = \dfrac{1}{2}DK.NE \Rightarrow DK = \dfrac{{2{S_{DNE}}}}{{NE}} = \dfrac{{a\sqrt {15} }}{6}$.

Ta có: $DK \bot \left( {SBC} \right) \Rightarrow DK \bot SK$.

$\Rightarrow \Delta SDK$ vuông tại $K$, suy ra $\sin \angle DSK = \dfrac{{DK}}{{SD}} = \dfrac{{\dfrac{{a\sqrt {15} }}{6}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{\sqrt 5 }}{3}$.

Vậy $\cos \alpha  = \sqrt {1 - {{\sin }^2}\alpha }  = \dfrac{2}{3}$.  

Chọn C.