Phương pháp giải:

- Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) suy ra \(SO \bot \left( {ABC} \right)\).

- Tính diện tích tam giác \(ABC\) bằng công thức Hê-rông: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của tam giác, \(p\) là nửa chu vi của tam giác.

- Sử dụng công thức tính bán kính đường tròn ngoại tiếp tam giác: \(R = \dfrac{{abc}}{{4S}}\).

- Áp dụng định lí Pytago tính đường cao của khối chóp.

- Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}{S_{day}}.h\).

Lời giải chi tiết:

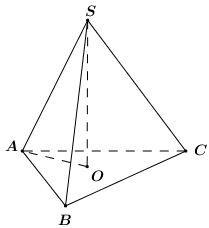
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Vì \(SA = SB = SC\,\,\left( {gt} \right)\) nên \(SO \bot \left( {ABC} \right)\).

Gọi \(p\) là nửa chu vi tam giác \(ABC\) ta có \(p = \dfrac{{AB + BC + CA}}{2} = \dfrac{{7a}}{2}\).

Suy ra \({S_{ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - CA} \right)}  = \dfrac{{3\sqrt 7 {a^2}}}{4}\).

\(OA\) là bán kính đường tròn ngoại tiếp \(\Delta ABC\) nên

\(OA = \dfrac{{AB.BC.CA}}{{4{S_{ABC}}}} = \dfrac{{2a.3a.2a}}{{4.\dfrac{{3\sqrt 7 {a^2}}}{4}}} = \dfrac{{4a\sqrt 7 }}{7}\).

Vì \(SO \bot \left( {ABC} \right)\) nên \(SO \bot OA\), do đó tam giác \(SOA\) vuông tại \(O\).

Áp dụng định lí Pytago trong tam giác vuông \(SOA\) ta có:

\(SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {3{a^2} - \dfrac{{16{a^2}}}{7}}  = \dfrac{{a\sqrt {35} }}{7}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}.SO.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {35} }}{7}.\dfrac{{3\sqrt 7 {a^2}}}{4} = \dfrac{{{a^3}\sqrt 5 }}{4}\).

Chọn D.