Phương pháp giải:

Biên độ dao động tại điểm cách nút sóng một đoạn d được xác định bởi:

${a_M} = 2a.\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|$

Với 2a là biên độ của điểm bụng

Tốc độ: $v = \dfrac{\lambda }{T} = \lambda f$

Lời giải chi tiết:

Biên độ dao động tại điểm cách nút sóng một đoạn d được xác định bởi:

${a_M} = 2a.\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|$

Với 2a là biên độ của điểm bụng

Điểm dao động với biên độ a: ${a_M} = 2a.\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right| = a \Rightarrow d = \dfrac{\lambda }{{12}}$

Vậy điểm dao động với biên độ a sẽ cách nút một khoảng: $d = \dfrac{\lambda }{{12}}$

x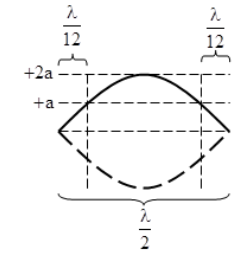

Khoảng cách gần nhất giữa hai điểm của hai bó sóng cạnh nhau có cùng biên độ là a sẽ là:

$\Delta x = 2.d = \dfrac{\lambda }{6} = 2cm \Rightarrow \lambda  = 12cm$

Tốc độ truyền sóng: $v = \lambda f = 12.5 = 60cm/s = 0,6m/s$

Chọn C.