Câu hỏi:
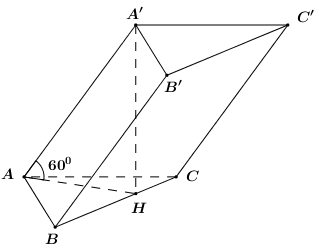
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(3a\). Hình chiếu của điểm \(A'\) lên \(\left( {ABC} \right)\) là điểm \(H\) thuộc cạnh \(BC\) sao cho \(BH = 2HC\). Cạnh bên tạo với đáy góc bằng \({60^0}\). Tính thể tích của khối lăng trụ \(ABC.A'B'C'\).
- A \(\dfrac{{9{a^3}\sqrt 3 }}{4}\)
- B \(\dfrac{{27{a^3}\sqrt 7 }}{4}\)
- C \(\dfrac{{6{a^3}\sqrt 6 }}{5}\)
- D \(\dfrac{{14{a^3}\sqrt 5 }}{3}\)
Phương pháp giải:
Khối nón cụt có đáy lớn \(R\), đáy nhỏ \(r\), chiều cao \(h\) có thể tích \(V = \frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right)\).
Lời giải chi tiết:
Vì \(A'H \bot \left( {ABC} \right)\) nên \(AH\) là hình chiếu của \(A'H\) lên \(\left( {ABC} \right)\).
Suy ra \(\angle \left( {A'A;\left( {ABC} \right)} \right) = \angle \left( {A'A;AH} \right)\) \( = \angle A'AH = {60^0}\).
Xét tam giác \(ABH\) có \(\angle ABH = \angle ABC = {60^0}\) (do tam giác \(ABC\) đều), \(AB = 3a,\) \(BH = \frac{2}{3}BC = 2a\).
Áp dụng định lí Cosin trong tam giác ta có:
\(\begin{array}{l}A{H^2} = A{B^2} + B{H^2} - 2AB.BH.\cos \angle ABH\\A{H^2} = {\left( {3a} \right)^2} + {\left( {2a} \right)^2} - 2.3a.2a.\cos {60^0}\\A{H^2} = 7{a^2}\end{array}\)
\( \Rightarrow AH = a\sqrt 7 \).
Vì \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot AH\) \( \Rightarrow \Delta A'AH\) vuông tại \(H\).
\( \Rightarrow A'H = AH.tan{60^0}\)\( = a\sqrt 7 .\sqrt 3 = a\sqrt {21} \).
Tam giác \(ABC\) đều cạnh \(3a\) nên \({S_{\Delta ABC}} = \frac{{{{\left( {3a} \right)}^2}\sqrt 3 }}{4} = \frac{{9{a^2}\sqrt 3 }}{4}\).
Vậy \({V_{S.ABC}} = \frac{1}{3}A'H.{S_{\Delta ABC}}\) \( = a\sqrt {21} .\frac{{9{a^2}\sqrt 3 }}{4} = \frac{{27\sqrt 7 {a^3}}}{4}\).
Chọn B.