Phương pháp giải:

Gọi cạnh tứ diện là \(x\), tính thể tích tứ diện theo \(x\) và \(r\), từ đó tìm \(x\).

Lời giải chi tiết:

Gọi cạnh tứ diện là \(x\).

Gọi \(O\) là tâm mặt cầu nội tiếp tứ diện, \(F\) là trọng tâm tam giác \(BCD\).

Thể tích tứ diện đều là: \(V = \dfrac{1}{3}{S_{BCD}}.AF\)

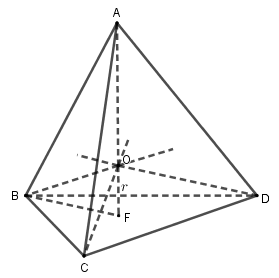
Ngoài ra \(V = {V_{O.BCD}} + {V_{O.ACD}} + {V_{O.ABD}} + {V_{O.ABC}}\)\( = 4{V_{O.BCD}} = 4.\dfrac{1}{3}OF.{S_{BCD}}\)

\( \Rightarrow 4.\dfrac{1}{3}OF.{S_{BCD}} = \dfrac{1}{3}{S_{BCD}}.AF \Leftrightarrow AF = 4OF = 4a\)

Ta có: \(BF = \dfrac{2}{3}.\dfrac{{x\sqrt 3 }}{2} = \dfrac{{x\sqrt 3 }}{3}\)\( \Rightarrow AF = \sqrt {A{B^2} - B{F^2}}  = \sqrt {{x^2} - \dfrac{{3{x^2}}}{9}}  = \dfrac{{x\sqrt 6 }}{3}\)

Mà \(AF = 4a \Rightarrow \dfrac{{x\sqrt 6 }}{3} = 4a \Leftrightarrow x = 2a\sqrt 6 \)

\( \Rightarrow \)\({S_{BCD}} = \dfrac{{{x^2}\sqrt 3 }}{4} = \dfrac{{{{\left( {2a\sqrt 6 } \right)}^2}.\sqrt 3 }}{4} = 6{a^2}\sqrt 3 \)

Vậy \(V = \dfrac{1}{3}AF.{S_{BCD}} = \dfrac{1}{3}.4a.6{a^2}\sqrt 3  = 8{a^3}\sqrt 3 \).

Chọn C.