Phương pháp giải:

- Tính thể tích mỗi khối chóp đỉnh \(M\) và đáy là các tam giác đều.

- Tính tổng thể tích và suy ra tổng khoảng cách từ \(M\) đến các mặt bên.

Lời giải chi tiết:

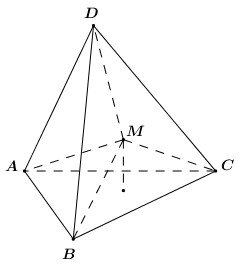
Xét tứ diện đều \(ABCD\), \(M\) là một điểm trong của nó.

Gọi \(V\) là thể tích, \(S\) là diện tích mỗi mặt của tứ diện đều \(ABCD\), \({h_A},{h_B},{h_C},{h_D}\) lần lượt là khoảng cách từ \(M\) đến các mặt \(\left( {BCD} \right),\left( {CDA} \right),\left( {DAB} \right),\left( {ABC} \right)\).

Ta có: \({V_{M.BCD}} = \dfrac{1}{3}S{h_A},{V_{M.CDA}} = \dfrac{1}{3}S{h_B},\) \({V_{M.DAB}} = \dfrac{1}{3}S{h_C},{V_{M.ABC}} = \dfrac{1}{3}S{h_D}\)

Khi đó ta có \(V = {V_{MBCD}} + {V_{MCDA}} + {V_{MDAB}} + {V_{MABC}}\)\( = \dfrac{1}{3}S\left( {{h_A} + {h_B} + {h_C} + {h_D}} \right)\)

\( \Rightarrow {h_A} + {h_B} + {h_C} + {h_D} = \dfrac{{3V}}{S}\).

Mà \(V,S\) là các số không đổi nên \({h_A} + {h_B} + {h_C} + {h_D}\) không đổi. (đpcm)