Phương pháp giải:

Trên các cạnh \(SA\) và \(SC\) lấy các điểm \(M,N\) sao cho \(SM = SN = SB = a\)

Tính thể tích của hình chóp đều \(S.BMN\)

Tính tỉ số thể tích \(\dfrac{{{V_{S.BMN}}}}{{{V_{S.ABC}}}}\) để tính thể tích của khối chóp \(S.ABC\)

Lời giải chi tiết:

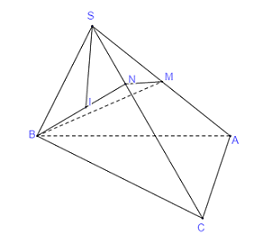
Trên các cạnh \(SA,SC\) lấy các điểm \(M,N\) sao cho \(SM = SN = SB = a\)

Hình chóp \(S.BMN\) có các cạnh bên \(SB = SM = SN\) nên chân đường cao hạ từ \(S\) xuống mp\(\left( {BMN} \right)\) là tâm đường tròn ngoại tiếp tam giác \(BMN\).

Tam giác \(SBN\) vuông tại \(S\) nên \(BN = \sqrt {S{B^2} + S{N^2}}  = \sqrt 2 a\)

Tam giác \(NSM\) có \(SN = SM\) và \(\widehat {NSM} = 60^\circ \) nên tam giác \(SMN\) là tam giác đều hay \(NM = a\)

Tương tự, \(BM = a\)

Tam giác \(BMN\) có \(B{M^2} + M{N^2} = B{N^2}\) nên tam giác\(BMN\) vuông tại M

Gọi \(I\) là trung điểm \(BN\) thì \(I\)  là tâm đường tròn ngoại tiếp tam giác \(BMN\)  hay \(SI \bot \left( {BMN} \right)\)

Ta có :

             \(\begin{array}{l}SI = \dfrac{1}{2}BN = \dfrac{{\sqrt 2 }}{2}a\\ \Rightarrow {V_{S.BMN}} = \dfrac{1}{3}SI.{S_{BMN}} = \dfrac{1}{3}.SI.\dfrac{1}{2}.NM.MB = \dfrac{1}{6}.\dfrac{{\sqrt 2 }}{2}a.a.a = \dfrac{{\sqrt 2 }}{{12}}{a^3}\end{array}\)

Lại có :

                 \(\dfrac{{{V_{S.BMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SB}}{{SB}}.\dfrac{{SN}}{{SC}}.\dfrac{{SM}}{{SA}} = 1.\dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6}\)

Do đó    \({V_{S.ABC}} = 6{V_{S.BMN}} = \dfrac{{\sqrt 2 }}{2}{a^3}\)

Chọn C.