Phương pháp giải:

- Gọi O là giao điểm của AC và BD. Chứng minh OA = OB = OC = OD = OS.

- Áp dụng định lí Pytago.

Lời giải chi tiết:

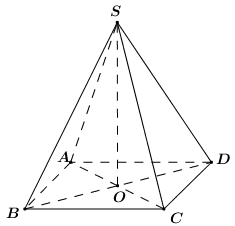
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên OA = OB = OC = OD.

Tam giác SAC vuông tại S có SO là trung tuyến ứng với cạnh huyền AC nên \(SO = \dfrac{1}{2}AC\) = OA = OC.

Suy ra OA = OB = OC = OD = OS nên O là tâm mặt cầu ngoại tiếp chóp S.ABCD và bán kính mặt cầu đó là R = OA.

Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \)\( = \sqrt {{a^2} + {a^2}} \)\( = a\sqrt 2 \).

Vậy \(R = \dfrac{{a\sqrt 2 }}{2} = \dfrac{a}{{\sqrt 2 }}\).

Đáp án A.