Phương pháp giải:

- Tìm chân đường cao của khối chóp đã cho.

- Xác định góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\), từ đó tính được chiều cao của hình chóp.

- Tính thể tích khối chóp \(V = \dfrac{1}{3}{S_{day}}.h\).

Lời giải chi tiết:

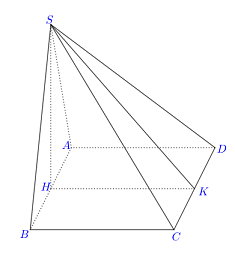
Gọi \(H\) là trung điểm của \(AB\).

\(\Delta SAB\) cân tại S nên \(SH \bot AB\).

Ta có : \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).

Gọi \(K\) là trung điểm \(CD \Rightarrow HK \bot CD\).

Ta có : \(\left\{ \begin{array}{l}CD \bot HK\\CD \bot SH\,\,\left( {SH \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow DCD \bot \left( {SHK} \right) \Rightarrow CD \bot SK\).

\(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SCD} \right) \supset SK \bot CD\\\left( {ABCD} \right) \supset HK \bot CD\end{array} \right. \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SK;HK} \right) = \angle SKH = {60^0}\)

Do \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot HK \Rightarrow \Delta SHK\) vuông tại \(H\).

Ta có: \(HK = AB = a \Rightarrow SH = HK.\tan \widehat {SKH} = a\sqrt 3 .\)

Vậy thể tích của khối chóp đã cho là \({V_{S.ABCD}} = \dfrac{1}{3}SH.AB.AD = \dfrac{{{a^3}\sqrt 3 }}{3}.\)

Chọn C.