Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = \sqrt 3 a,\,\,AD = a,\,\,\Delta SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo \(a\) diện tích \(S\) của mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
- A \(S = 5\pi {a^2}\)
- B \(S = 10\pi {a^2}\)
- C \(S = 4\pi {a^2}\)
- D \(S = 2\pi {a^2}\)
Phương pháp giải:
Lời giải chi tiết:
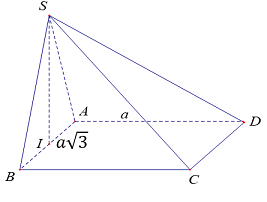
\( + )\)Xét \(\Delta SAB\)đều: Gọi \(I\)là trung điểm \(AB \Rightarrow SI \bot \left( {ABCD} \right).\)
Gọi \(G\) là trọng tâm tam giác \(SAB\) ta có: \(SI = \dfrac{{\sqrt 3 }}{2}.a\sqrt 3 = \dfrac{3}{2}a\)
\( \Rightarrow GS = GA = GB = \dfrac{2}{3}.SI = a\).
\( + )\)Xét \(\Delta ABC\) vuông tại \(B\) có:\(A{B^2} + B{C^2} = A{C^2}\) (Định lí Pytago)
\( \Leftrightarrow {\left( {a\sqrt 3 } \right)^2} + {a^2} = A{C^{^2}} \Rightarrow AC = 2a.\)
\( + )\)Xét hình chữ nhật \(ABCD\): gọi \(O = AC \cap BD\).
\( \Rightarrow OA = OC = OB = OD = \dfrac{{AC}}{2} = \dfrac{{2a}}{2} = a\).
\(\begin{array}{l} \Rightarrow R = \sqrt {G{S^2} + O{A^2} - \dfrac{{A{B^2}}}{4}} = \sqrt {{a^2} + {a^2} - \dfrac{{{{\left( {a\sqrt 3 } \right)}^2}}}{4}} = \dfrac{{\sqrt 5 }}{2}a\\ \Rightarrow {S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {\dfrac{{\sqrt 5 }}{2}a} \right)^2} = 5\pi {a^2}.\end{array}\)
Chọn A


















