Câu hỏi:
Cắt hình nón đỉnh \(S\) bởi mặt phẳng đi qua trục, ta được một tam giác vuông cân có cạnh huyền bằng \(2a\). Thể tích của khối nón là:
- A \(\dfrac{{\pi {a^3}\sqrt 2 }}{{12}}\)
- B \(\dfrac{{\pi {a^3}}}{3}\)
- C \(\dfrac{{\pi {a^3}\sqrt 2 }}{2}\)
- D \(\pi {a^3}\)
Phương pháp giải:
Lời giải chi tiết:
+ Thiết diện qua trục là\(\Delta ABC\)vuông cân tại \(A\) có \(BC = 2a\)
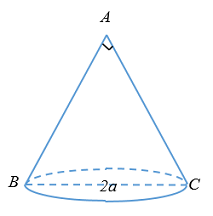
\( \Rightarrow R = \dfrac{1}{2}BC = \dfrac{1}{2}.2a = a.\)
+ Gọi \(O\) là trung điểm \(BC\).
+ \(h = AO = \dfrac{1}{2}BC = a\) (tam giác vuông có đường trung tuyến bằng nửa cạnh huyền).
\( \Rightarrow \) \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}\).
Chọn B
Quảng cáo
Câu hỏi trước
