Phương pháp giải:

Lời giải chi tiết:

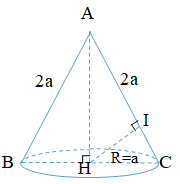
+ Gọi chân đường cao hạ từ \(H\) xuống \(AC\) là \(I\).      

\( \Rightarrow HI\) là khoảng cách từ tâm của đáy hình nónđến đường sinh.                

+ Vì \(\Delta ABC\) đều cạnh \(2a\)\( \Rightarrow AH = 2a\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)

+ Xét \(\Delta AHC\) vuông tại \(H\) có:

\(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{C^2}}}\)

\( \Leftrightarrow \dfrac{1}{{H{I^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow HI = \dfrac{{3{a^2}}}{4} \Rightarrow HI = \dfrac{{a\sqrt 3 }}{2}\)

Chọn B