Câu hỏi:
Cho lăng trụ đứng \(ABC.A'B'C'\), đáy \(ABC\) là tam giác vuông cân tại \(A\). \(E\) là trung điểm của \(B'C',\,\,CB'\) cắt \(BE\) tại \(M\). Tính thể tích \(V\) của khối tứ diện \(ABCM\) biết \(AB = 3a,\,\,AA' = 6a\):
- A \(V = 6{a^3}\)
- B \(V = 6\sqrt 2 {a^3}\)
- C \(V = 8{a^3}\)
- D \(V = 7{a^3}\)
Phương pháp giải:
Lời giải chi tiết:
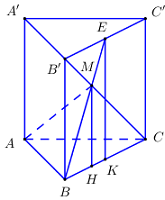
Kẻ \(MH \bot BC,\,\,EK \bot BC\).
Ta có: \(\Delta B'ME \sim \Delta CMB\,\,\left( {g.g} \right) \Rightarrow \dfrac{{ME}}{{MB}} = \dfrac{{B'E}}{{CB}} = \dfrac{1}{2}\).
\(\begin{array}{l}\Delta BHM \sim \Delta BKE\,\,\left( {g.g} \right) \Rightarrow \dfrac{{MH}}{{KE}} = \dfrac{{BM}}{{BE}} = \dfrac{2}{3}\\ \Rightarrow MH = \dfrac{2}{3}EK = \dfrac{2}{3}.6a = 4a\end{array}\)
\(V = \dfrac{1}{3}MH.{S_{\Delta ABC}} = \dfrac{1}{3}.4a\left( {\dfrac{1}{2}.3a.3a} \right) = 6{a^3}\).
Chọn A
Quảng cáo
Câu hỏi trước
