Phương pháp giải:

Lời giải chi tiết:

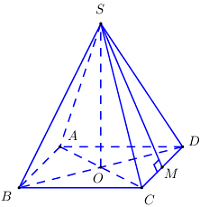
Gọi độ dài các cạnh của hình chóp là \(x\).

\( \Rightarrow SM = a = \dfrac{{x\sqrt 3 }}{2} \Rightarrow x = \dfrac{{2a}}{{\sqrt 3 }} = \dfrac{{2a\sqrt 3 }}{3}\).

\({S_{ABCD}} = {\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)^2} = \dfrac{{4{a^2}}}{3}\).

\(SO = \sqrt {S{M^2} - O{M^2}}  = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt 6 }}{3}\) 

\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{4{a^2}}}{3} = \dfrac{{4{a^3}\sqrt 6 }}{{27}}\).

Chọn B