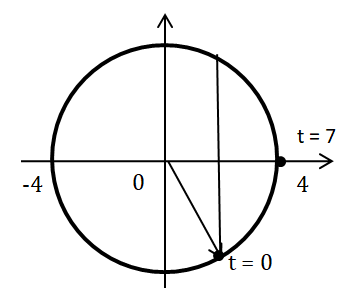Câu hỏi:
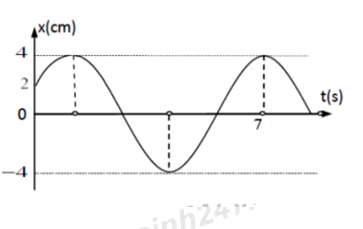
Đồ thị dao động của một chất điểm dao động điều hòa như hình vẽ. Phương trình biểu diễn sự phụ thuộc của vận tốc của vật theo thời gian là:
- A \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)\,\,\left( {cm/s} \right)\).
- B \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{6}t + \frac{{5\pi }}{6}} \right)\,\,\left( {cm/s} \right)\).
- C \(v=4\pi \cos \left( \frac{\pi }{3}t+\frac{\pi }{3} \right)\,\,\left( cm/s \right)\).
- D \(v = 4\pi \cos \left( {\frac{\pi }{6}t + \frac{\pi }{3}} \right)\,\,\left( {cm/s} \right)\).
Phương pháp giải:
Phương trình vận tốc của dao động: \(v = - A\omega \sin \left( {\omega t + \varphi } \right) = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\).
Lời giải chi tiết:
Từ đồ thị, nhận xét A = 4 cm.
Tại thời điểm t = 0, vật ở li độ x = 2 cm chuyển động về biên dương → \(\varphi = - \frac{\pi }{3}\).
Tại thời điểm t = 7 s, \(\Delta \varphi = 2\pi + \frac{\pi }{3} = \frac{{7\pi }}{3} \Rightarrow \omega = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{{7\pi }}{3}}}{7} = \frac{\pi }{3}\left( {rad/s} \right)\).
Phương trình vận tốc: \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)\,\,\left( {cm/s} \right)\).
Chọn A.