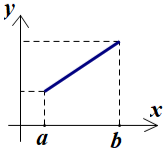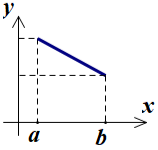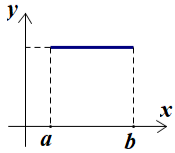Phương pháp giải:

Cho hàm số \(y = f\left( x \right)\) xác định trên \(\left( {a;b} \right)\).

Khi đó hàm số \(y = f\left( x \right)\)  đồng biến trên \(\left( {a;b} \right)\) nếu \(\forall {x_1},{x_2} \in \left( {a;b} \right):{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right).\)

Khi đó hàm số \(y = f\left( x \right)\)  nghịch biến trên \(\left( {a;b} \right)\) nếu \(\forall {x_1},{x_2} \in \left( {a;b} \right):{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right).\)

Lời giải chi tiết:

Lấy 2 giá trị \({x_1},{x_2}\) sao cho \(a < {x_1} < {x_2} < b\).

Xét các đáp án ta thấy với \(a < {x_1} < {x_2} < b,\) chỉ có đồ thị ở đáp án A là có \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right).\) 

Chọn  A.