Câu hỏi:
ABCD.A’B’C’D’ là hình lập phương cạnh a. Thể tích khối tứ diện A’BDC’ là:
- A \(\frac{{{a^3}\sqrt 3 }}{2}\)
- B \(\frac{a^3}{3}\)
- C \(\frac{2a^3}{3}\)
- D \(\frac{{{a^3}\sqrt 6 }}{4}\)
Phương pháp giải:
Lời giải chi tiết:
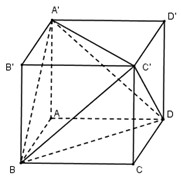
Ta có: \({V_{ABCD.A'B'C'D'}} = {a^3}\)
\({V_{B.A'B'C'}} = \dfrac{1}{3}BB'.S{ _{A'B'C'}} = \dfrac{1}{3}BB'.\dfrac{1}{2}A'B'.B'C' = \dfrac{1}{6}{a^3}\)
Tương tự ta có \({V_{C'.BCD}} = {V_{D.A'C'D'}} = {V_{A'.ABD}} = \dfrac{1}{6}{a^3}\)
\({V_{A'BDC'}} = {V_{ABCD.A'B'C'D'}} - {V_{B.A'B'C'}} - {V_{C'.BCD}} - {V_{D.A'C'D'}} - {V_{A'.ABD}} = {a^3} - 4.\dfrac{1}{6}{a^3} = \dfrac{1}{3}{a^3}\)
Chọn B.
Quảng cáo
Câu hỏi trước
