Câu hỏi:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
- A \(\dfrac{{{a^3}}}{6}\)
- B \(\dfrac{{{a^3}}}{3}\)
- C \(\dfrac{{{a^3}}}{4}\)
- D \(\dfrac{{{a^3}}}{8}\)
Phương pháp giải:
Lời giải chi tiết:
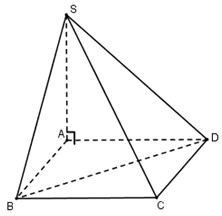
Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)
\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Chọn A.
Quảng cáo
Câu hỏi trước
