Câu hỏi:
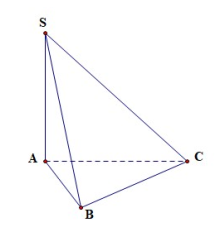
Cho hình chóp \(S.ABC\) có SA vuông góc với mặt phẳng (ABC), \(SA = 2a\), tam giác ABC vuông tại B, \(AB = a\), \(BC = a\sqrt 3 \). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng
- A \({90^o}\).
- B \({30^o}\).
- C \({60^o}\).
- D \({45^o}\).
Phương pháp giải:
Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa \(d\) và \(d'\) với \(d'\) là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\)
Sử dụng tỉ số lượng giác của góc nhọn để suy ra số đo góc.
Lời giải chi tiết:
Ta có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\)
\( \Rightarrow \)\(A\) là hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\)
\( \Rightarrow \)\(AC\) là hình chiếu của \(SC\) lên mặt phẳng \(\left( {ABC} \right)\)
Từ đó góc giữa \(SC\) và mặt phẳng \(\left( {ABC} \right)\) là \(\widehat {SCA}\)
Vì \(\Delta ABC\) vuông tại B \( \Rightarrow A{C^2} = A{B^2} + B{C^2} = {a^2} + 3{a^2} = 4{a^2}\)\( \Rightarrow AC = 2a\)
Xét tam giác \(SAC\) vuông tại \(A\) có \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{2a}}{{2a}} = 1 \Rightarrow \widehat {SCA} = {45^o}\).
Vậy góc cần tìm bằng \(45^\circ .\)
Chọn D.